Esercizio
Assegnato il campo vettoriale in coordinate sferiche
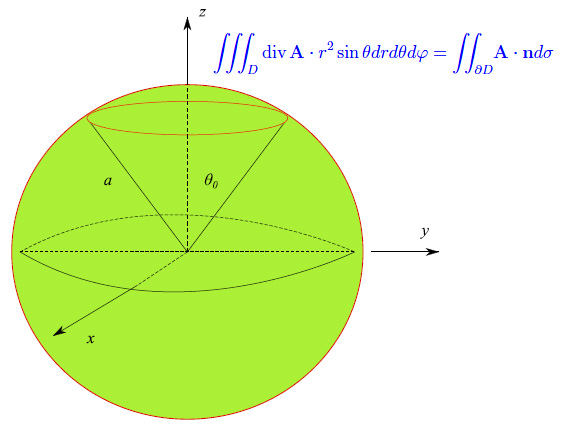
verificare il teorema della divergenza per il seguente dominio
per un'assegnata colatitudine θ0, come illustrato in fig. 1
Soluzione
Rammentando l'espressione dell'elemento di volume in coordinate sferiche, si ha che il teorema della divergenza nel caso in esame si scrive:
Poniamo
Per determinare la divergenza del campo vettoriale assegnato, utilizziamo la nota formula
ottenendo
Segue
Cioè
Passiamo ora al secondo integrale. La frontiera di D può scriversi:
dove S1 ha la ovvia rappresentazione parametrica
Il versore n1 è ortogonale a S1 ed è orientato verso l'esterno di D, onde
Una rappresentazione parametrica della superficie S2 è
Il versore n2 è ortogonale a S2 ed è orientato verso l'esterno di D, onde è manifestamente
L'elemento di superficie su S2 è
essendo
l'angolo solido elementare, per cui
Ciò implica
Ne concludiamo
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)