Ricapitoliamo, correggendo, i risultati dell' esercizio precedente. Stiamo considerando una resistenza ohmica R sottoposta a una d.d.p. di durata τ:
calcolandone la trasformata di Fourier:
La potenza istantanea dissipata per effetto Joule è
Denotando con E(t) l'energia dissipata all'istante t, si ha:
onde
In particolare, l'energia totale dissipata è:
Più in generale, i.e. per una qualunque V(t) di modulo quadro sommabile in (-oo,+oo), si ha
Per l'uguaglianza di Parseval
Introducendo lo spettro di potenza:
si ha
La funzione di autocorrelazione è definita dalla coppia di trasformate integrali:
Segue
Tutto ciò suggerisce:
L'espressione corretta è
dove η definisce un intervallo di tempo. Consideriamo ora l'esempio di una d.d.p. con un andamento del tipo onda quadra:
La trasformata di Fourier è:
Gli integrali si calcolano facilmente:
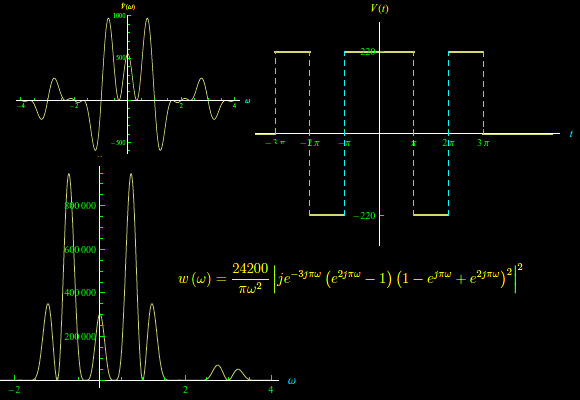
Lo spettro di potenza
i grafici sono riportati in fig. 1.
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)