[¯|¯] Gli zeri non banali della zeta di Riemann e la "striscia critica"

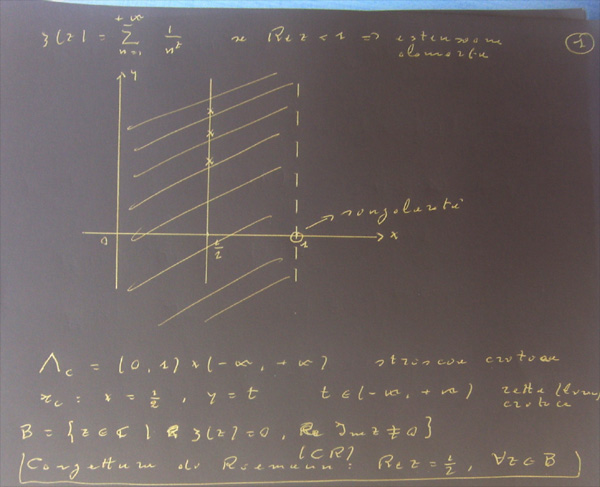
È stato dimostrato che se la congettura di Riemann è falsa, gli zeri non banali della funzione zeta di Riemann cadono nella cosiddetta "striscia critica":

Un modo per dimostrare (o confutare) la congettura consiste nel "parametrizzare" la restrizione della zeta a una assegnata retta parallela all'asse immaginario e contenuta nella striscia critica, studiano poi la distribuzione degli zeri delle funzioni (reali) date rispettivamente da parte reale e parte immaginaria della predetta restrizione. Ci si può svincolare dalle funzioni n^-i*t passando agli esponenziali complessi.