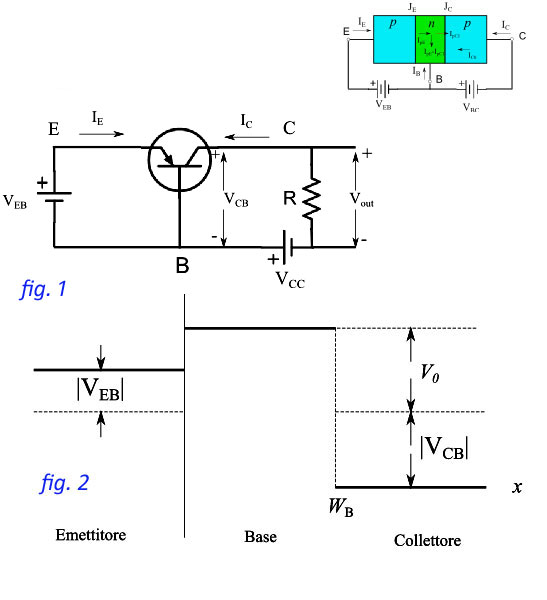
Esaminiamo da un punto di vista per così dire microscopico, quanto esposto nei numeri precedenti. Per essere più specifici, consideriamo un transistor pnp nelle due configurazioni 1) assenza di polarizzazione; 2) polarizzazione diretta della giunzione JE, polarizzazione inversa della giunzione JC.
Nel caso 1, come sappiamo dalla teoria della giunzione, a cavallo di JC si stabilisce una d.d.p. di contatto V0 che ha (con buona approssimazione) un andamento a gradino come illustrato in fig.
dove consideriamo giunzioni simmetriche i.e. di pari dimensione fisica e concentrazione del drogaggio.
Siamo dunque in presenza di una cosiddetta barriera di potenziale che abbiamo già trattato nella nostra piattaforma, sia a livello di meccanica classica che a livello di meccanica quantistica. Di seguito alcuni link di approfondimento:
- Particella (quantistica) vincolata a un segmento con barriera di potenziale
- Effetto tunnel. Il concetto di Istantone
- Allargamento della barriera di potenziale
- Coefficiente di trasmissione
- Barriera di potenziale deltiforme
- Barriera di potenziale parabolica
Nelle regioni E e C le cariche libere non hanno energia sufficiente per attraversare la barriera. Cioè eB. Nel caso 2 la configurazione di polarizzazione è schematizzata in fig. 1. Ciò determina una rottura di simmetria della barriera di potenziale di contatto. Precisamente, per x=0 la barriera è abbassata di |VEB}|, mentre per x=0 risulta alzata di |VCB}|. L'andamento del potenziale è in fig. 2.
Discutiamo le singole regioni:
per cui un numero macroscopico di lacune ha energia sufficiente per attraversare la barriera in corrispondenza della giunzione JC. Il campo elettrico è ovviamente
per cui su JE è una delta di Dirac:
Su JC
Ne segue che il campo elettrico accelera le lacune che attraversano la giunzione JC (buca di potenziale), per cui vengono «raccolte» dal collettore.