Problema di Cauchy per un sistema autonomo del primo ordine
Consideriamo il seguente problema di Cauchy:
con f funzione lipschitziana in X (intervallo limitato di R). Per una nota proprietà delle equazioni differenziali che si integrano per separazione di variabili, il non annullarsi di f in x0, implica che dobbiamo escludere la soluzione costante x(t)=x0, e quindi eseguire una quadratura per separazione di variabili:
essendo C una costante di integrazione. Denotando con G(x) una primitiva della reciproca di f(x), si ha che l'integrale generale dell'equazione differenziale è implicitamente definito da:
Classe di soluzioni monotòne e limitate
Siamo interessati alle soluzioni del problema proposto nella sezione precedente, che siano funzioni monotonamente crescenti e limitate superiormente, per cui
La richiesta di monotonia implica
Ne segue
e x=λ è manifestamente uno zero di f. Infatti, dal momento che la retta orizzontale x=λ è asintoto orizzontale a destra, si ha:
Quindi
e siccome f è continua in [0,λ], ne segue che x=λ è uno zero. Dall'equazione differenziale segue
Cioè l'integrale a primo membro diverge, per cui la funzione 1/f(x) è nel limite per x->λ- un infinito di ordine maggiore o uguale di 1. Da ciò segue che la funzione f(x) è per x->λ- un infinitesimo di ordine maggiore o uguale di 1.
Analisi nel dominio delle configurazioni
Se il sistema dinamico in istudio modellizza un processo fisico che avviene nel tempo discreto (si consideri, ad esempio, un modello epidemiologico), allora il problema di Cauchy si riscrive:
dove
A tale equazione (alle differenze finite) si perviene facilmente scrivendo l'equazione differenziale nella forma:
Campionando la variabile continua t e assumendo unitario l'intervallo di campionamento:
e quindi l'equazione scritta più sopra, che viene risolta per ricorrenza nel piano xnxn+1. Un esempio molto noto è la mappa logistica:
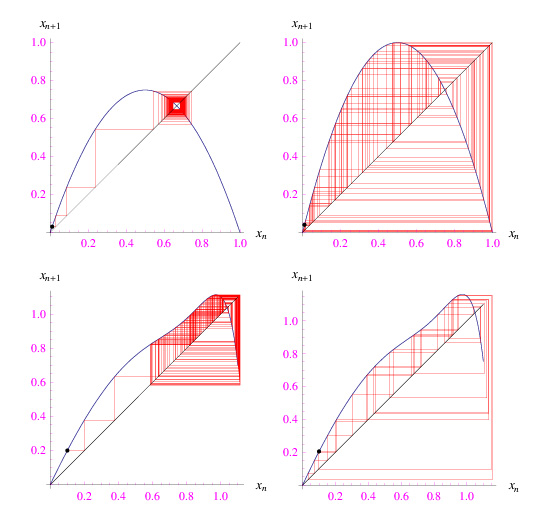
in cui α > 0 è un parametro assegnato. L'evoluzione è caotica a partire da α=3.5. Da simulazioni in Mathematica ritroviamo il caos deterministico per il sistema iterato dal polinomio
dove ß varia da 2.0 a 2.15. In occasione di quest'ultimo valore, si innesca il caos deterministico, come vediamo dai grafici di fig. 1.