Esercizio
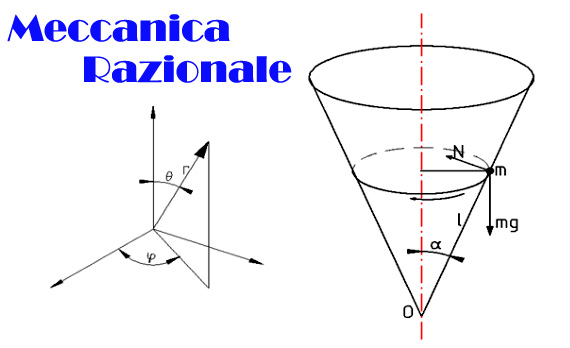
Una particella di massa m è costretta a muoversi, senza attrito, sulla superficie interna di un cono (fig. 1).
a) Trovare le condizioni per cui la particella descrive un'orbita circolare.
b) Verificare la stabilità dell'orbita.
Soluzione
In coordinate sferiche (r,θ,φ) le equazioni del moto sono:
Poiché la particella è costretta a muoversi sulla superficie interna del cono, si ha:
Pertanto la prima delle equazioni del moto si scriverà:
Per il moto in un'orbita circolare attorno al suo asse verticale si ha
Con l=l0 si ha
Essendo
possiamo chiamare
La particella ha una velocità tangenziale v0 all'orbita
Dunque
che è la condizione iniziale che deve essere soddisfatta da v0 e da l0.
Quesito b
Si supponga una piccola perturbazione sulla particella tale che
L'equazione del moto ricavata in precedenza diventa:
Segue
Trascurando i termini di ordine superiore al primo per le quantità
si può scrivere:
ma per conto dell'equazione scritta più sopra il membro di destra si annulla. Dunque:
Non ci sono forze tangenziali agenti sulla particella in moto; pertanto non vi sono momenti torcenti rispetto all'asse verticale e il momento angolare rispetto allo stesso asse è costante:
da cui
avendo trascurato i termini di ordine superiore al primo. Pertanto l'equazione scritta più sopra diviene
Il termine in parentesi è reale e positivo; l'equazione è quella di un semplice oscillatore armonico, da cui la stabilità dell'orbita.
No TweetBacks yet. (Be the first to Tweet this post)