[¯|¯] Un Modello epidemiologico basato su un'equazione differenziale stocastica

Modifichiamo l'equazione differenziale precedente nel modo che segue

Ricordiamo che g(t) rappresenta l'azione farmacologica. Per quanto riguarda l'altra funzione, assumiamo

Ne consegue che

rappresenta l'assenza di azioni farmacologiche. Tale configurazione restituisce la classica crescita esponenziale:

essendo N₀ la popolazione inizialmente infettata. Viceversa

restituisce un decadimento esponenziale, per cui la pandemia si annulla in tempi relativamente brevi. Uno scenario più realistico è implementato da un'azione farmacologica "rumorosa". Nello specifico, possiamo considerare un Brown Noise i.e. un White Noise filtrato, con un andamento del tipo di quello riportato in fig.

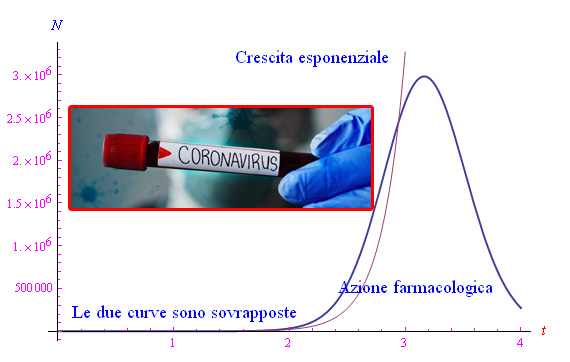
Ne consegue una natura stocastica dell'equazione differenziale che regola l'andamento della funzione N(t). Tuttavia, un Brown Noise può essere simulato nell'ambiente di calcolo Mathematica per cui la predetta equazione differenziale può essere risolta in tale ambiente. In fig. 1 riportiamo una soluzione per un'assegnata condizione iniziale N₀ =N(0), da cui vediamo che a tempi brevi la crescita della popolazione infetta avviene con legge esponenziale, dopodichè si raggiunge un massimo assoluto, per poi tendere a zero.