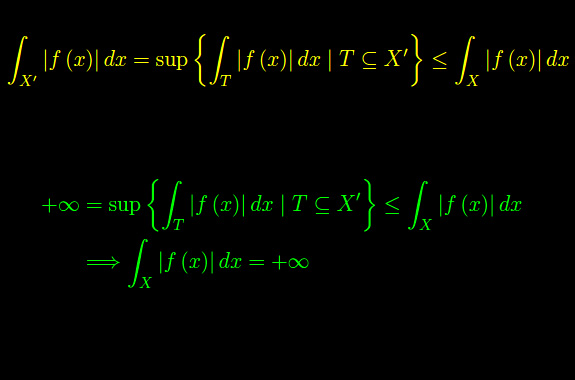
Il teorema appena dimostrato è di scarsa utilità nei casi pratici. Tuttavia, permette di dimostrare delle condizioni sufficienti di di sommabilità, attravero la formulazione di tre criteri.
Criterio 1
Sia
una funzione generalmente continua in X contenuto in R. Se X è limitato e f(x) è limitata, allora f(x) è ivi sommabile.
Dim.
Se f(x) è limitata, comunque prendiamo T contenuto in X che sia di continuità per f(x), si ha:
onde
Posto
si ha
onde l'asserto (dal teorema)
Criterio 2
Siano
generalmente continue in X (limitato o illimitato), e tali che
Segue
Dim.
Lasciata per esercizio.
Criterio 3
Sia f(x) generalmente continua in X (limitato o illimitato).
Dim.
Lasciata per esercizio.
Sostienici
Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.
No TweetBacks yet. (Be the first to Tweet this post)