Per quanto visto in una lezione precedente ad un assegnato numero complesso z=x+iy corrisponde univocamente un punto P del piano complesso (o piano di Gauss). Detto punto si dice affissa del numero complesso z, e quest'ultmo è la sua immagine. Passando dalle coordinate cartesiane (x,y) alle coordinate polari (ρ&theta), comunque prendiamo z=0 i.e. P distinto dall'origine O, si ha:
In tal modo l'affissa di P si esprime:
che definisce la forma trigonometrica del numero complesso z. Si ha:
onde
Ne consegue che il raggio vettore dell'immagine P di z, è il modulo di z.
Definizione
Dicesi argomento di z e si denota con arg(z), l'anomalia del punto P immagine di z.
Dal momento che l'anomalia è definita a meno di multipli interi di 2π, si ha che tale sarà arg(z). Se, invece, ci riferiamo all'anomalia principale, si ha l'argomento principale e si denota con Arg(z).
Rammentando che il polo O del riferimento polare i.e. l'origine del riferimento cartesiano del piano di Gauss, ha anomalia indeterminata si ha che arg(0) è indeterminata.
Lemma
Assegnati i numeri complessi
si ha
Dimostrazione
L'asserto segue immediatamente applicando le formule di addizione degli archi.
Il risultato precedente si generalizza al prodotto di n numeri complessi:
avendosi
Teorema di Moivre
Dimostrazione
L'asserto discende direttamente dal lemma dimostrato in precedenza, per
Definizione
La formula appena dimostrata è nota come formula di Moivre.
Poniamo per definizione
Inoltre, la formula di Moivre può essere generalizzata ad esponenti negativi:
che può essere riscritta come
In particolare
onde il raggio vettore e l'anomalia del reciproco di un numero complesso z=0, sono dati rispettivamente dal reciproco del raggio vettore di z e dall'opposto dell'anomalia di z. A sua volta ciò implica che dati i numeri complessi:
si ha:
Esempio
Determiniamo il reciproco del numero complesso z=1+i. Innanzitutto passiamo alla rappresentazione trigonometrica;
L'argomento principale è:
onde
Segue
Cioè
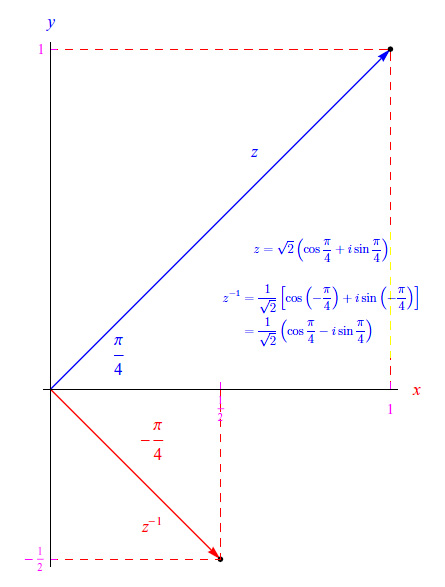
In fig. 1 rappresentiamo graficamente il numero complesso z=1+i e il suo reciproco z-1.
Sostienici