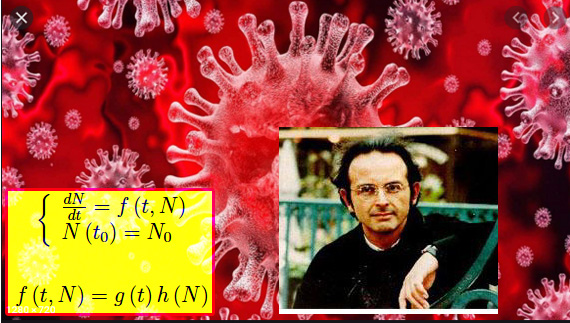
I sistemi dinamici del tipo mappa logistica che descrivono l'evoluzione di una popolazione di individui (insetti, batteri, virus), sono sistemi autonomi.
Più precisamente, se N(t) è la popolazione a un istante generico t, si ha che in questi modelli, tale funzione è una soluzione del seguente problema di Cauchy
dove f(N) è un'assegnata funzione lipschitziana.
Dalla teoria delle equazioni differenziali, sappiamo che una tale equazione è autonoma, nel senso che f non dipende esplicitamente dal tempo. Dal momento che la mappa logistica deriva da un caso particolare del problema scritto più sopra, i predetti sistemi sono autonomi. Ciò consente di passare alla corrispondente equazione alle differenze finite, che va risolta ricorsivamente in modo da riprodurre le ben note proprietà di tali sistemi attraverso la ricerca di fixed points(e quindi, attrattori, ergodicità, caoticità, etc.).
"Autonomia del sistema" vuol dire fondamentalmente, che la sua evoluzione temporale è governata esclusivamente dalla dinamica interna. I fattori esterni (le risorse dell'ambiente) agiscono da modulatori dell'espressione analitica della funzione f(N) che determina il tasso di crescita/decrescita. In altre parole tali fattori agiscono indirettamente.
Nel paradigma dell'autopoiesi di Maturana--Varela,un sistema autonomo è autopoietico, nel senso che riesce a riprodurre parte di sé senza un intervento esterno. Tale creazione è generata dalla predetta dinamica interna. Per essere più precisi, tale dinamica determina la chiusura organizzativa del sistema. Quindi un sistema autopoietico è energicamente aperto (nella misura in cui dipende dall'ambiente) ed organizzativamente chiuso (nella misura in cui riesce a creare parte di sé). Matematicamente, la chiusura organizzativa si realizza attravero l'autonomia dell'equazione differenziale
mentre l'apertura energetica si esprime tramite una dipendenza implicita dal tempo. Precisamente, se N(t) è un'integrale di tale equazione differenziale, si ha:
Le medesime considerazioni possono essere applicate al caso di una epidemia/pandemia di carattere virale. In questo caso specifico, N(t) è la grandezza che esprime il numero di infezioni in funzione del tempo. Se si adotta un modello del tipo mappa logistica:
si ha che tale sistema è, per dirla con Maturana e Varela, autopoietico per cui si comporta alla stregua di un organismo vivente (sistema energicamente aperto e organizzativamente chiuso). D'altra parte, un intervento farmacologico può essere matematicamente rappresentato da una funzione f(N) tale che
Ne consegue che per t»t* ci si aspetta N(t)~0. Tuttavia, è matematicamente più corretto rappresentare un intervento preventivo (farmacologico e altro) attraverso un meccanismo matematico che rende il sistema organizzativamente aperto, i.e. allopoietico ovvero non-autonomo:
Precisamente:
essendo g(t) la funzione che rappresenta l'intervento farmacologico. Integrando per separazioni di variabili, si ottiene una rappresentazione implicita della grandezza N(t):
dove H(N) è una primitiva di h(N)-1.