[¯|¯] Smorzamento esponenziale dell'onda termica

venerdì, Ottobre 12th, 2018

trasmissione del calore, onda termica,metodo di fourier — **fig. 1**

Nel testo Teoria ed applicazioni della serie di Fourier e in Differential equations and root cellars: [applications of differential equations to physics] sono riportati due procedimenti distinti, entrambi basati sulla serie di Fourier, per dimostrare che la cantina ideale deve trovarsi a 4.5 metri di profondità. Infatti, in tal caso l'onda termica è in opposizione di fase rispetto al profilo in superficie. Entrambi i procedimenti sono indipendenti dall'oscillazione in superficie, nel senso che si considera una qualunque funzione u₀(t) periodica di periodo T=365 giorni.
(altro…)

Posted in News | No Comments »

[¯|¯] L'equazione di conduzione del calore. Caso unidimensionale. Il metodo di Fourier

giovedì, Ottobre 11th, 2018

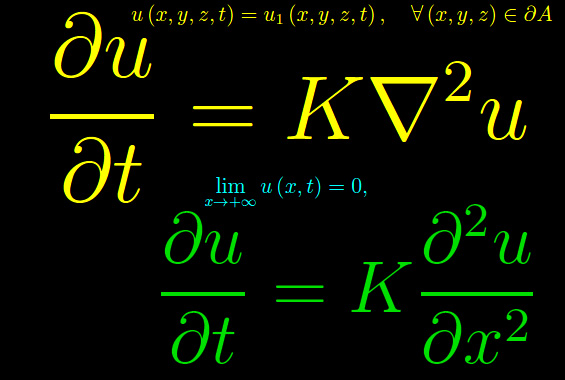
equazione di conduzione del calore,condizioni al contorno,equazioni differenziali alle derivate parziali,metodo di fourier

Premessa

L'ottimizzazione termica di una cantina è un difficile problema di Fisica Matematica, le cui origini si perdono nella notte dei tempi. Incidentalmente, per cantina termica ideale si intende una classe di soluzioni dell'equazione differenziale alle derivate parziali che regola la conduzione del calore dalla superficie terrestre verso una quota assegnata nella verticale passante per un punto della superficie della Terra, ed orientata verso il centro del pianeta (in approssimazione sferica).
(altro…)