[¯|¯] Equazione della corda vibrante. La soluzione di D'Alembert

martedì, Ottobre 16th, 2018

quazione della corda vibrante,equazioni differenziali alle derivate parziali,soluzione di D'Alembert

Introduzione

Molti processi fisici sono caratterizzati da una grandezza scalare u(x,y,z,t) funzione delle coordinate x,y,z e del tempo t, quale soluzione di una equazione differenziale alle derivate parziali (PDE, da qui in avanti). Senza perdita di generalità, consideriamo il caso unidimensionale nelle coordinate spaziali, i.e. u(x,t).

Siamo interessati ai processi fisici che possono essere descritti da PDE del secondo ordine e lineari:

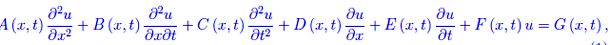
dove A(x,t),B(x,t),... sono assegnate funzioni sufficientemente regolari, denominate coefficienti dell'equazione, mentre G(x,t) è il termine noto. Se le A(x,t),...,F(x,t), si riducono a delle costanti, l'equazione si dirà a coefficienti costanti. Se poi G(x,t)=0, l'equazione è omogenea.
(altro…)