Energia Negativa | » Esercizi svolti di Matematica e Fisica

Il problema dell'energia negativa e delle «onde anticipate» di Fantappiè

sabato, Aprile 24th, 2021

luigi fantappiè,onde anticipate,energia negativa

Abbiamo visto che in uno stato di impulso definito, il corrispondente autovalore dell'energia è dato da:

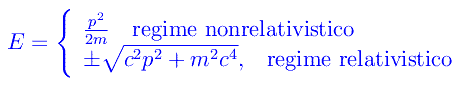
da cui constatiamo la comparsa di stati ad energia negativa per una particella relativistica. Ciò pone seri problemi interpretativi, poiché classicamente l'energia di una particella libera è non negativa. In ogni caso, la corrispondente funzione d'onda si scrive:

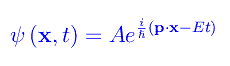
Come è noto, l'energia può essere espressa in termini di frequenza angolare:

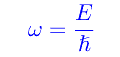
per cui la richiesta di non negatività dell'energia appare «sensata». Si osservi che ciò non si limita ai soli autostati dell'energia: una qualunque sovrapposizione di autostati dell'energia deve presentare termini a «frequenza positiva». Roger Penrose, nel suo libro La strada che porta alla realtà, espone questo problema attraverso un'estensione dell'analisi di Fourier nel campo complesso. Per comprendere questa estensione, facciamo l'esempio banale della serie di Fourier. Precisamente (utilizziamo la notazione di Penrose), sia f(ξ) una funzione reale della variabile reale ξ, e di periodo l. Se sono verificate le condizioni di Dirichlet, possiamo scrivere

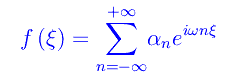
che è l'usuale sviluppo in serie di Fourier. Qui abbiamo introdotto la frequenza ω=2ω/l.
L'estensione al campo complesso si realizza introducendo la variabile complessa z=exp(i*ωξ), per cui lo sviluppo in serie di Fourier si riscrive:

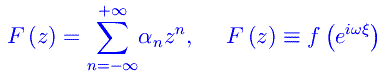
che ci ricorda lo sviluppo di Laurent della funzione complessa F(z). Topologicamente, l'estensione al campo complesso si realizza trasformando l'intervallo di periodicità [0,l] nella circonferenza centrata nell'origine e di raggio l. Attraverso argomentazioni basate sull'Analisi complessa, Penrose riesce a "selezionare" nel campo complesso le componenti a «frequenza positiva» da quelle a «frequenza negativa».

A questo punto, potrebbe esserci un legame tra questa richiesta (delle frequenze positive) con la nozione di onda ritardata di Fantappiè, esposta in un numero precedente.