L'equazione d'onda di Klein-Gordon
Aprile 22nd, 2021 | by Marcello Colozzo |
Ricordiamo che lo stato quanto-meccanico di una particella nonrelativistica di massa m è una soluzione dell'equazione di equazione di Scrhoedinger che qui scriviamo in forma operatoriale:
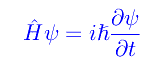
dove
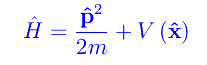
è l'operatore hamiltoniano, mentre ψ è la funzione d'onda della particella. Rammentiamo velocemente la rappresentazione dei vari operatori nella base delle coordinate
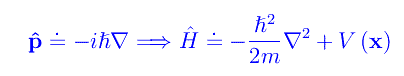
per cui ritroviamo la ben nota forma dell'equazione di Scrhödinger:
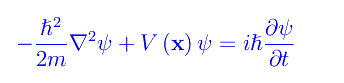
Per scrivere un'equazione d'onda relativistica, prendiamo spunto dalla seguente sostituzione formale:
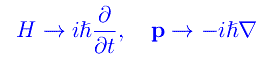
Qui H è la funzione hamiltoniana della particella. Dalla meccanica relativistica, sappiamo che per una particella libera
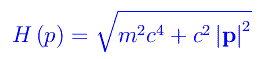
onde
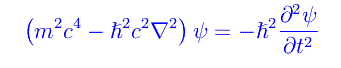
ossia
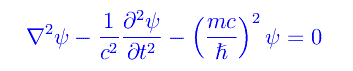
nota come equazione di Klein-Gordon. Si noti che se non ci fosse il terzo termine a primo membro, la K-G sarebbe la equazione di D'Alembert. Un'altra differenza notevole rispetto a quella di Schrödinger è che la K-G è del secondo ordine nella derivata temporale. E ciò presenterà problemi interpretativi
Dopo qualche manipolazione, si giunge all'equazione di continuità per la grandezza
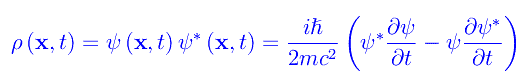
Precisamente
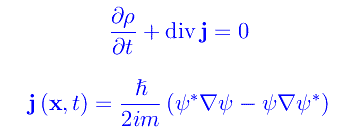
Siamo tentati a chiamare ρ «densità di probabilità», ma la presenza della derivata seconda rispetto al tempo nella K-G porta a una inconsistenza. Precisamente, dal momento che l'equazione del secondo ordine e «somiglia» alla D'Alembert, si ha che un problema di Cauchy è caratterizzato da condizioni iniziali (con ovvio significato dei simboli):
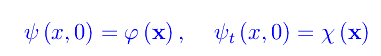
dove le funzioni sono assegnate ad arbitrio. Ciò implica che la grandezza ρ non è definita positiva, per cui non è una densità di probabilità. Una possibile re-interpretazione consiste nel ridefinire:
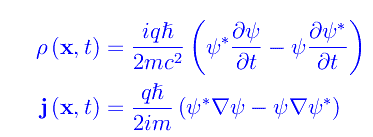
essendo q la carica elettrica (eventualmente nulla) della particella. Siamo interessati alle soluzioni del tipo onda piana monocromatica che come è noto, sono stati quantistici con valore definito dell'impulso. Senza ledere la generalità, consideriamo il caso unidimensionale:
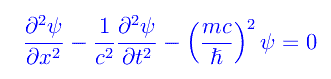
Cerchiamo soluzioni del tipo
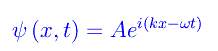
Dopo qualche passaggio
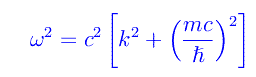
Moltiplicando primo e secondo membro per la costante ridotta di Planck e rammentando la relazione tra pulsazione ed energia, e tra numero d'onde ed impulso, si ha
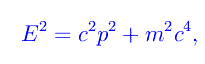
cioè proprio quello che ci si aspetta. Più precisamente, poniamo
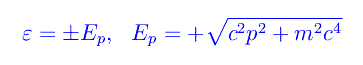
Ne segue che allo stesso autovalore dell'impulso corrispondono due stati con energia diversa:
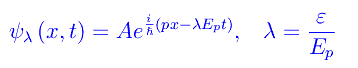
Precisamente:

No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











