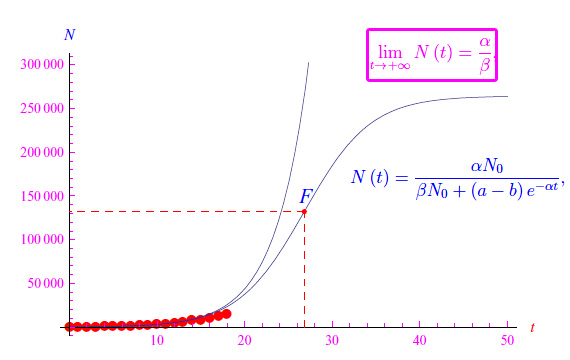
Esaminiamo l'approccio standard per la ricerca di una logistica per il sistema dinamico in esame. Come è noto, si assegna un'equazione differenziale del tipo Riccati che nel nostro caso si scrive:
dove α è il valor medio dei vari parametri calcolati in precedenza, mentre ß > 0 è un parametro ignoto che agisce da fattore di smorzamento dell'esponenziale. Integrando tale equazione differenziale con la condizione iniziale N(0)=N0=221, dopo qualche passaggio si ottiene:
da cui emerge il comportamento asintotico:
e il comportamento esponenziale a tempi brevi. Con i dati in nostro possesso presi dal sito web della Protezione civile, abbiamo visto che un valore affidabile del parametro ß è
Infatti, plottando la soluzione otteniamo l'andamento riportato in fig. 1. Inoltre, studiando la derivata seconda si stabilisce l'esistenza di un punto di flesso a tangente obliqua, visibile nella predetta figura. L'ascissa è
corrispondente al 31 marzo.
No TweetBacks yet. (Be the first to Tweet this post)