Coronavirus. La crescita esponenziale vista nelle spazio delle configurazioni

Se la fase attuale della diffusione del virus è di carattere esponenziale, significa che il numero di contagiati N(t) risolve il problema di Cauchy:

dove α > 0. Assumendo come istante iniziale t₀ la data del 24/02/2020, dal sito web della Protezione civile possiamo prendere il numero di contagiati per ogni giorno successivo. Questo significa che dobbiamo passare dall'equazione differenziale scritta sopra alla corrispondente equazione alle differenze finite. Scriviamo:

dove dobbiamo prendere come minimo intervallo di tempo Δ=1 d , quindi

Più precisamente, prendiamo il valore medio:

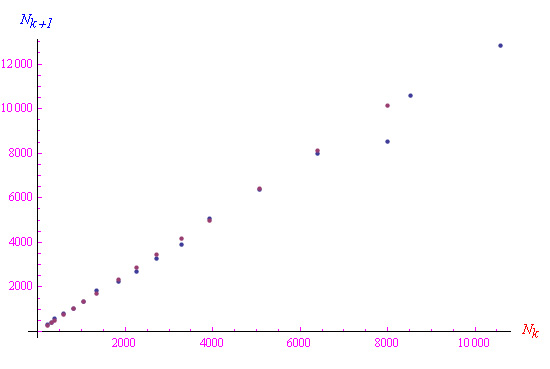
A questo punto studiamo l'evoluzione dinamica del sistema nello spazio delle configurazioni definito dal piano cartesiano (N_k,N_k+1). Utilizzando i dati presi dal sito web citato sopra, otteniamo il diagramma delle orbite di fig. 1 dove i pallini blue sono i dati reali, mentre quelli rossi compongono il diagramma delle orbite del sistema la cui funzione di trasferimento è tale che:

Quest'ultima definisce l'evoluzione dinamica di un sistema a crescita esponenziale. Dal momento che i diagrammi delle orbite sono quasi sovrapposti, si deduce che il regime di diffusione del coronavirus è in fase di crescita esponenziale.