[¯|¯] Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

giovedì, Novembre 2nd, 2017

Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

Definizione
Sia data la funzione:

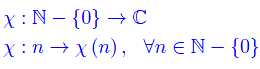
Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

Si definisce serie di Dirichlet associata alla predetta funzione, la serie:

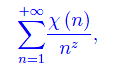
Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

dove z=x+iy è l'usuale variabile complessa.
Enunciamo alcuni teoremi e proprietà omettendone la dimostrazione.
Teorema
Hp.

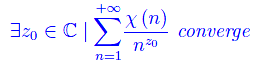
Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

Th. La serie di Dirichlet converge in

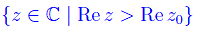
Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

e denotiamo la sua somma con:

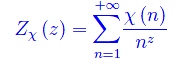
Serie di Dirichlet. La funzione zeta di Riemann-Eulero e la funzione di Riemann-Siegel

(altro…)



Posted in Funzioni di una variabile complessa | No Comments »