Forma trigonometrica degli integrali ellittici
mercoledì, Aprile 21st, 2021
In questo numero eseguiamo un cambio di variabile che trasforma gli integrali ellittici di prima, seconda e terza specie. Iniziamo con gli integrali di prima specie:

rammentando che P(x) è un polinomio di terzo grado. Ed è chiaro che possiamo scriverlo nella forma:

assumendo i coefficienti reali. Supponiamo poi che le radici siano reali: α,ß,γ. Si noti che per i nostri scopi, tali radici devono essere distinte. Diversamente:

per cui

che non è un integrale ellittico. Assumiamo poi la seguente convenzione:

e in entrambi i casi, ß è la radice media. Più formalmente:

Senza perdita di generalità, consideriamo il caso (+):

(altro…)

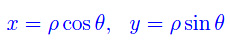
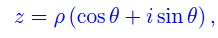
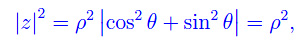


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
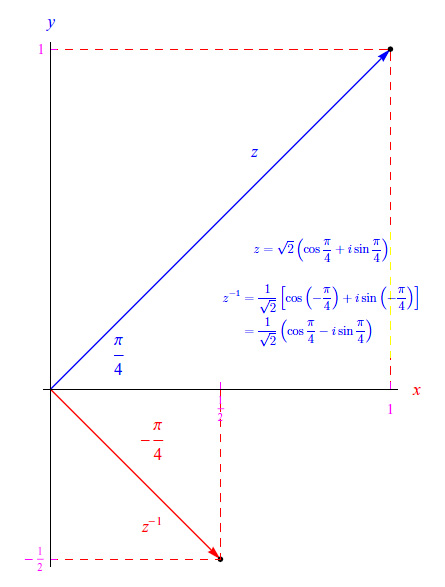
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











