Barriera Di Potenziale | » Esercizi svolti di Matematica e Fisica

Barriera di potenziale. «Caduta» verso il centro

martedì, Aprile 13th, 2021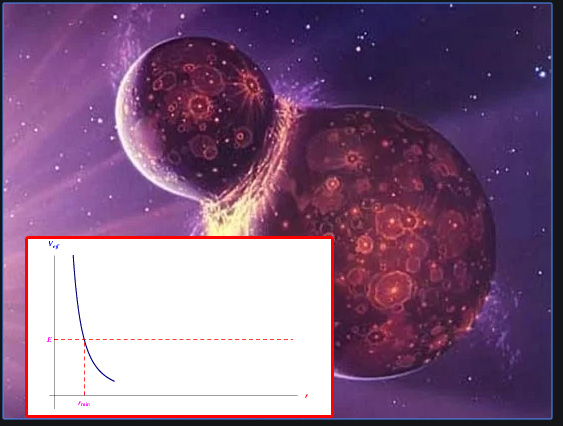

Riprendiamo l'esempio suggestivo della Luna, dove avevamo stabilito l'impossibilità di una «caduta» radiale del nostro satellite sulla Terra. Restando nell'approssimazione di campo centrale, mostriamo una ulteriore impossibilità: il passaggio della Luna per il centro di forza, i.e. per la Terra. In altre parole, vogliamo stabilire l'eventuale esistenza di orbite passanti per il centro di forza. A tale scopo, riprendiamo l'equazione differenziale:

dove ci riferiamo al caso generale di una particella di massa m, rammentando l'espressione del potenziale efficace che si esprime come somma del potenziale centrale e del potenziale centrifugo:

da cui notiamo che il termine centrifugo è una barriera di potenziale infinitamente alta. Ne segue che il potenziale efficace è a sua volta una barriera di potenziale infinitamente alta, per tutti e soli i potenziali V(r) tali che

Infatti in fig.

vediamo che in tal caso, la particella non può «penetrare» la barriera di potenziale. In altri termini, il potenziale impedisce la «caduta» verso in centro, e ciò si verifica per ogni valore dell'energia E > 0. Si badi che tale locuzione si riferisce a una caduta sia radiale che angolare.
Il potenziale efficace diverge per i potenziali V(r) continui in r=0 (o al più con una discontinuità eliminabile):

e per quelli divergenti positivamente:

Studiamo i potenziali divergenti negativamente:

osservando che i potenziali di interesse fisico divergenti negativamente in r=0, sono ivi infiniti dotati di ordine. Per fissare le idee, consideriamo un potenziale V(r) tale che in un intorno destro di r=0 si comporta come

Ne segue

per α=2

(altro…)

Posted in Meccanica analitica, Meccanica celeste, meccanica razionale | No Comments »

[¯|¯] Particella (quantistica) vincolata a un segmento con barriera di potenziale

giovedì, Agosto 2nd, 2018

meccanica quantistica, problemi unidimensionali,segmento,barriera di potenziale — **Fig. 1**

Il testo di questo esercizio è tratto da Fondamenti di meccanica quantistica con esercizi e soluzioni, mentre la soluzione è nostra. Abbiamo comunque notato delle incongruenze nella soluzione riportata nel testo, riguardo alla ricerca per via grafica degli autovalori dell'energia.

In questo esercizio una particella è vincolata all'asse x che è sede di un campo di forze con potenziale riportato in fig. 1

Determinare i valori di V₀ tali che l'hamiltoniana ammetta V₀ come autovalore, con autofunzione costante non nulla per x in [-b,b].
Determinare V₀ in modo che E=V₀ sia il livello fondamentale e scrivere la corrispondente autofunzione.
Per il valore V₀ di cui al punto precedente, scrivere l'equazione che determina implicitamente l'energia degli stati eccitati.

(altro…)