Curve di fase e curve separatrici

Novembre 25th, 2020 | by Marcello Colozzo |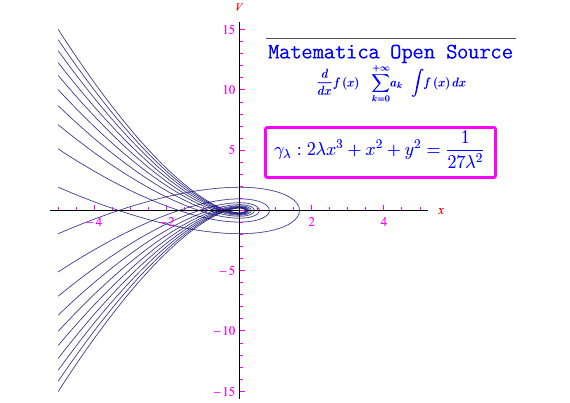

curve di fase, curve separatrici — **Fig. 1**

Completiamo l'esercizio precedente determinando le equazioni delle curve di fase e delle separatrici.
Le prime sono:

per un assegnato valore di E. Per λ ->0

cioè una famiglia di circonferenze di centro l'origine e raggio v(2E) con E > = 0. Ovviamente questo è il caso dell'oscillatore armonico che solitamente ha per curve di fase una famiglia di ellissi. Qui invece, dal momento che la massa della particella e la costante elastiche sono entrambe pari a 1, le ellissi sono circonferenze. Si noti che per E=0 la curva di fase degenera nell'origine, giacché x=0 è di equilibrio stabile. Per λ > 0 abbiamo la famiglia di curve del terzo ordine scritta più sopra.
L'unica separatrice è

Il nome deriva dal fatto che ogni separatrice è composta da due rami divergenti. Al variare del coefficiente perturbativo otteniamo una famiglia di curve in parte plottata in fig. 1.

No TweetBacks yet. (Be the first to Tweet this post)