» Esercizi svolti di Matematica e Fisica

Well-posedness del problema (Stabilità dei sistemi di controllo)

Le ipotesi di osservabilità e controllabilità ci assicurano che {A,B,C,D} è una realizzazione minima del sistema lineare, cui corrisponde una G(s) razionale propria. La funzione φ(·) deve essere tale che il sistema a ciclo chiuso possieda una soluzione unica: una condizione sufficiente affinchè l'equazione dx/dt=Ax-Bφ(·)(Cx), nel caso D=0, abbia una soluzione unica è che la funzione φ(·) sia almeno Lipschitz in un intorno dello zero (condizione di esistenza ed unicità locale). Nel caso D diverso da 0 occorre aggiungere una condizione più restrittiva. Si deve verificare anche che la relazione ingresso-uscita

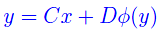
abbia una unica soluzione y=h(x): se la funzione φ(·) è monotona si può dimostrare che y=Cx+Dφ(y) possiede un'unica soluzione y=h(x) per ogni x appartenente a Rⁿ [1].

La condizione di appartenenza ad un settore, che implica φ(0)=0, assicura che l'origine x=0 è un punto di equilibrio del sistema a ciclo chiuso.

Tags: lipschitz, stabilità dei sistemi di controllo, well-posedness del problema