Metodo dei minimi quadrati: implementazione in Mathematica (parte 1)
Aprile 23rd, 2020 | by Marcello Colozzo |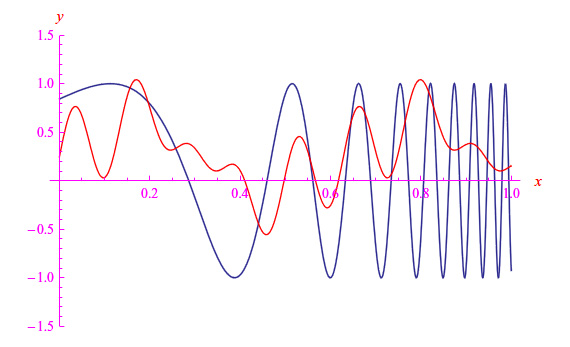
Per minimizzare l'errore quadratico medio per un generico ordine di approssimazione n, conviene studiare l'espressione generale:

Per determinare gli eventuali punti estremali di tale funzione reale delle n+1 variabili reali c0,...,c_{n}, dobbiamo risolvere il sistema di equazioni

A tale scopo, esplicitiamo il primo membro

Calcoliamo a parte

dove troviamo la delta di Kronecker:

onde

Quindi

Ne consegue che il sistema precedente si riscrive

Cioè

Se poniamo

riesce

Per maggiore chiarezza

In altri termini, i punti estremali della predetta funzione sono tutte e sole le soluzioni (se esistono) del sistema di n+1 equazioni lineari nelle n+1 incognite c0,c1,...,c1. Studiamo allora, la matrice dei coefficienti e la matrice dei coefficienti+termini noti:

Per il teorema di Rouche-Capelli:

Come è noto, il rango della matrice dei coefficienti è la caratteristica del sistema e solitamente si indica con p. Siccome tale matrice è quadrata di ordine n+1, allora p < =n+1. Se poi richiediamo anche l'unicità della soluzione, allora deve essere p=n+1. Ne segue

Rammentando l'espressione degli elementi di matrice di A, si ha che dobbiamo scegliere le n+1 funzioni φj(x) in modo da generare una matrice A non singolare. Verificata questa condizione, per la determinazione delle incognite si applica la nota regola di Cramer:

essendo Δi il determinante di ordine n+1 ottenuto da detA sostituendo la colonna i-esima con quella dei termini noti ((n+1)-esima colonna della matrice B). A titolo di esempio, riprendiamo la funzione f(x)=sin(e^{4x}) e applichiamo il procedimento appena esposto con le funzioni

Risolvendo il sistema con Mathematica, otteniamo per la somma approssimante, il grafico di fig. 1.
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











