[¯|¯] Approssimazione "locale" di una funzione. Lo sviluppo di Taylor

Aprile 21st, 2020 | by Marcello Colozzo |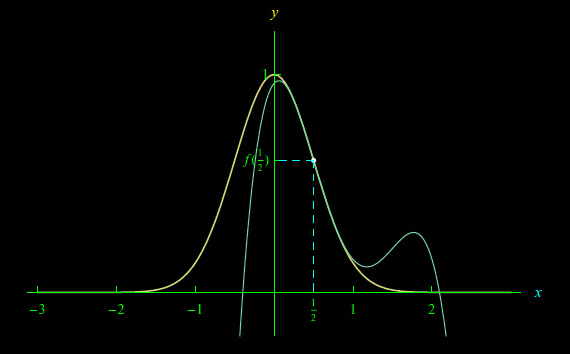

approssimazione,funzione,sviluppo di taylor — **Fig. 1**

Da una serie di osservazioni sperimentali sufficientemente accurate, ricaviamo i valori assunti da una grandezza y in funzione di una variabile reale x. Precisamente:

Senza perdita di generalità, si supponga il seguente ordinamento:

Ci proponiamo di approssimare la funzione f attraverso un numero assegnato di funzioni note o meglio, mediante una appropriata combinazione lineare:

dove φ_k(x) sono le predette funzioni. In tale procedimento di approssimazione appare naturale definire l'errore:

È chiaro che l'approssimazione è buona se l'errore è "trascurabilmente piccolo". Quest'ultima locuzione dipende dalla natura dell'approssimazione cercata. Ad esempio, se stiamo ricercando un'approssimazione locale, i.e. in un intorno di un punto x_k della sequenza scritta più sopra, dobbiamo imporre:

Cioè

che è un sistema di n+1 equazioni lineari nelle n+1 incognite c₀,c₁,...,c_n. Tale sistema sotto ovvie condizioni, permette di determinare l'unica n-pla (c₀,c₁,...,c_n) che rende minimo l'errore in un intorno di x_k. Ad esempio, lo sviluppo di Taylor di punto iniziale x_k e troncato al termine di ordine n+1, corrisponde manifestamente alla scelta di funzioni

ovvero i polinomi di grado 0,1,2,...,n. Come esempio numerico, consideriamo la gaussiana:

il cui sviluppo in serie di Taylor di punto iniziale 1/2 troncato al termine di ordine 4 è la seguente combinazione lineare di polinomi:

In fig. 1 riportiamo il grafico della f(x) confrontato con la predetta combinazione lineare, da cui vediamo che l'approssimazione è buona in un intorno di 1/2.

No TweetBacks yet. (Be the first to Tweet this post)