La diffusione virale quale integrale di un processo di Wiener |

La diffusione virale quale integrale di un processo di Wiener

Aprile 9th, 2020 | by Marcello Colozzo |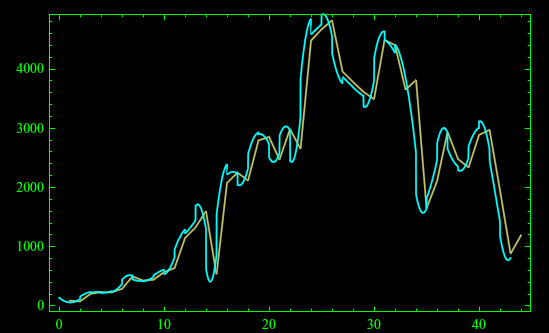

coronavirus,processo di wiener,rumore bianco,rumore brown — **Fig. 1**

Denotiamo con η(t) il numero di attualmente positivi nell'istante t. Per quanto precede, la variabile tempo è in realtà campionata con intervallo di campionamento Δ=1d , a partire da t₀ = 0=24/02. Plottando i dati η_k e interpolando otteniamo il grafico di figura:

in cui confrontiamo η_k con η(t).

La versione per così dire, discreta, della derivata prima di η(t) è η_k+1-η_k giacché è Δ=1. Plottando queste differenze in funzione di t_k=k, otteniamo

Avendo a disposizione la funzione η(t) ottenuta per interpolazione, possiamo confrontare il grafico della derivata prima con quelle delle differenze finite (fig. 1). L'affidabilità del processo di interpolazione suggerisce di determinare la derivata seconda, ottenendo il grafico

Anche se i dati sono pochi, tale andamento ricorda quello di un rumore bianco. Proviamo allora ad eseguire un'analisi spettrale della derivata seconda. A rigore, dovremmo prima determinare le differenze delle differenze, e da questi dati eseguire una DFT (con Mathematica) sui dati ottenuti. Il risultato è in figura:

da cui vediamo la presenza di alcuni picchi. Incidentalmente, il primo picco compare anche nella derivata prima, e risulta amplificato. Tuttavia, se l'argomentazione precedente è corretta, ci aspettiamo la comparsa di nuovi picchi con il trascorrere dei giorni, fino a quando avremo una densità di picchi non nulla, il che equivale a dire che la derivata seconda è un rumore bianco (giacché ogni frequenza contribuisce con lo stesso peso statistico al segnale).

Una prima conclusionè è dunque, la seguente: