[¯|¯] Immagine di un'applicazione vettoriale
Febbraio 4th, 2020 | by Marcello Colozzo |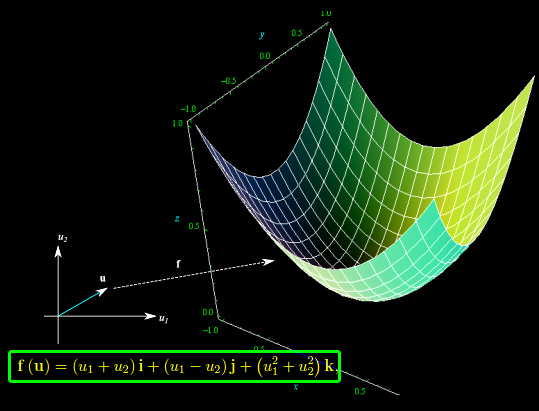
Alle funzioni vettoriali, quali applicazioni tra spazi vettoriali, si applicano le definizioni di suriettiva, iniettiva, bi-iettiva. In particolare:
Definizione
Assegnata una funzione vettoriale f:E->F, dicesi immagine di E attraverso f , l'insieme
Tale sottoinsieme di F è anche noto come immagine dell'applicazione f (anziché dello spazio vettoriale E).
Osservazione
Si badi che in generale, f(E) non è un sottospazio vettoriale di F. Come vedremo in seguito ciò si verifica solo per una particolare classe di applicazioni.
Esercizio
Determinare l'immagine della funzione vettoriale:

così definita

dove {i,j,k} è la base canonica di R³, mentre

con {e1,e2} base canonica di R².
Soluzione
Per definizione di immagine:

Ciò implica che le componenti della funzione vettoriale assegnata, nelle basi assegnate, sono

Ma

onde

Eliminando le variabili u1,u2:

che è l'equazione di un paraboloide ellittico. Ne concludiamo che l'immagine dell'applicazione assegnata, è il predetto paraboloide (fig. 1)
Tags: Funzioni vettoriali di una variabile vettoriale, Immagine di un'applicazione vettoriale, paraboloide ellittico
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











