[¯|¯] Funzioni vettoriali di una variabile vettoriale
Febbraio 4th, 2020 | by Marcello Colozzo |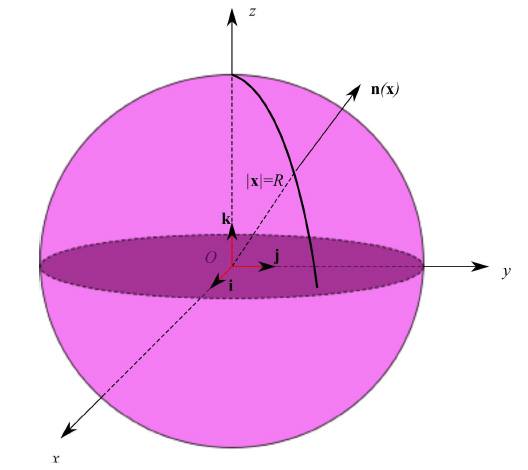
Nelle lezioni precedenti abbiamo introdotto la nozione di rappresentazione parametrica (avente per base un assegnato aperto U di R²) di una superficie S, per poi osservare che quest'ultima è l'immagine di un'applicazione che associa univocamente ad ogni elemento di U, un elemento di S. Ne consegue che la nozione di rappresentazione parametrica "parla" il linguaggio delle funzioni (naturalmente intese come legge di corrispondenza tra due insiemi).
Nello specifico, gli elementi di U sono vettori di un assegnato sottospazio vettoriale dello spazio euclideo bidimensionale (R²) , mentre una qualunque superficie S è un sottoinsieme dello spazio euclideo tridimensionale R³, ma non un suo sottospazio vettoriale. Vediamo, dunque, che nella definizione di rappresentazione parametrica di una superficie, sono coinvolti gli spazi vettoriali (euclidei) R² e R³. Ne consegue che la predetta rappresentazione parametrica altro non è che una legge di corrispondenza tra tali spazi vettoriali. È preferibile comunque, riferirsi a spazi vettoriali (finito-dimensionali) su un qualunque campo K.
Incidentalmente, sussiste la seguente definizione:
Definizione
Siano E e F due spazi vettoriali (finito-dimensionali) su uno stesso campo K. Un'applicazione (o funzione vettoriale) di E in F, è una legge di corrispondenza simboleggiata da:
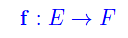
che associa univocamente a ogni vettore x di E, un vettore y di F. Quindi:
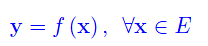
Abbiamo detto che E,F sono finito-dimensionali. Cioè
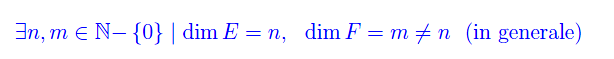
Siano
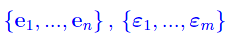
due basi di E e F rispettivamente. Segue
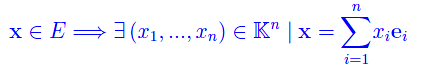
Cioè la n-pla di scalari

definisce le componenti di x nella predetta base. Allo stesso modo:
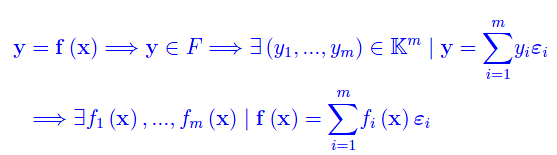
Definizione
Le m funzioni scalari delle n variabili scalari
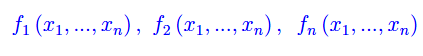
sono le componenti della funzione vettoriale f(x) nelle basi assegnate di E ed F.
Esempio
Nello spazio euclideo R³ consideriamo una sfera S di raggio R e di centro l'origine O di riferimento cartesiano ortogonale (Oxyz), come in fig. 1. Dalla geometria analitica sappiamo che la rappresentazione cartesiana di S è:
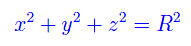
vettorialmente equivalente a

Qui x è il vettore posizione di un generico punto di R³, espanso nella base ortonormale {i,j,k}. Denotando con n il versore di un generico x di S, è facile convincersi che n è il versore della retta normale a S orientata dall'interno verso l'esterno della sfera. Segue
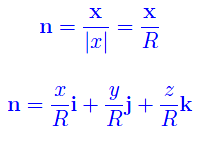
D'altra parte
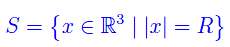
i.e. è un sottoinsieme (ma non un sottospazio vettoriale) di R³. Quindi n(x) è una funzione vettoriale della variabile vettoriale x, e

Tags: Funzioni vettoriali di una variabile vettoriale, Geometria differenziale, rappresentazione parametrica, superficie
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











