» Esercizi svolti di Matematica e Fisica

[¯|¯] Disequazioni razionali intere di secondo grado

Gennaio 23rd, 2020 | by Marcello Colozzo |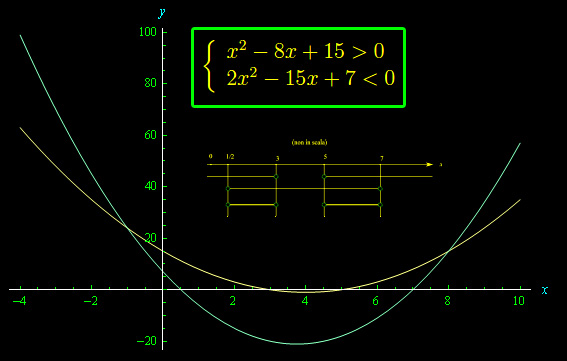

Approfittiamo ora per risolvere alcune disequazioni razionali intere dei secondo grado. (Esercizi tratti dal Zwirner --Analisi matematica 1. La soluzione è nostra).

---

Esercizio 1
Risolvere la disequazione

Soluzione
Determiniamo innanzitutto il discriminante: Δ=-19 < 0 per cui la disequazione assegnata è priva di soluzioni nel campo reale. Graficamente, la parabola y=x²-x+5, non interseca l'asse x:

---

Esercizio 2
Determinare i valori del parametro reale m, per i quali l'equazione

ammette radici reali.
Il discriminante dell'equazione è










Dobbiamo imporre

Le radici dell'equazione sono

Quindi

che è l'intervallo di valori reali di m che risolvono il problema dato. In fig. riportiamo alcune parabole della famiglia

---

Esercizio 3
Per quali valori del parametro reale m la disequazione

è soddisfatta per ogni x?
Soluzione
Il discriminante deve essere negativo:

Quindi

La corrispondente equazione ha radici

Ne consegue che deve essere

---

Esercizio 4
Risolvere il sistema di disequazioni

Soluzione
Risolviamo la prima, determinando prima le radici della corrispondente equazione

Quindi l'insieme delle soluzioni della prima disequazione è

Passiamo alla seconda, calcolando prima le radici dell'equazione

Segue

L'insieme delle soluzioni del sistema è l'intersezione degli insiemi trovati:

Può essere utile il grafico seguente

Tags: disequazioni razionali intere di secondo grado

Articoli correlati