[¯|¯] Ramanujan e la funzione zeta di Riemann

Settembre 4th, 2019 | by Marcello Colozzo |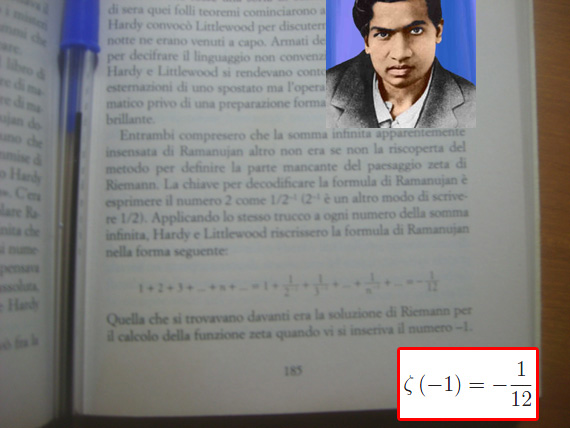

ramanujan,numeri primi,funzione zeta di riemann — **Fig. 1**

Dal libro L'enigma dei numeri primi, visualizziamo la formula in fig. 1, che riscriviamo di seguito

Il primo membro può essere scritto come:

che ovviamente diverge. Tuttavia, nel libro è scritto (il punto interrogativo è nostro):

come stabilito da Ramanujan. Qui mancano una infinità di passaggi (quindi la genialità di Ramanujan). Precisamente, dobbiamo scrivere (z=x+iy è l'usuale variabile complessa):

La serie a secondo membro è la serie di Dirichlet che definisce la funzione zeta di Riemann, valutata in z=-1:

Tale serie converge per x > 1, per cui siamo d'accordo con il risultato precedente. Ma la somma di questa serie può essere estesa per continuazione analitica (o prolungamento analitico) su tutto il piano complesso ad eccezione di z=1, dove troviamo una singolarità polare di ordine 1 (polo semplice). Riemann ottenne l'espressione seguente: