» Esercizi svolti di Matematica e Fisica

[¯|¯] Il lato oscuro dello sviluppo di Hadamard

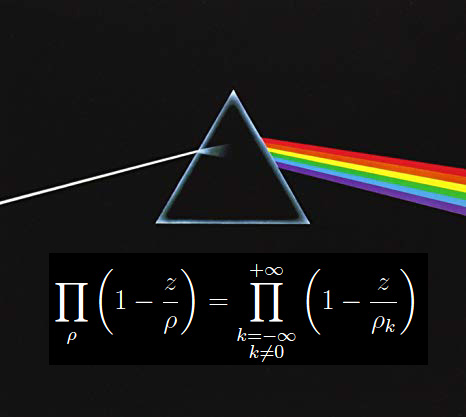
Per quanto stabilito nel numero precedente, lo sviluppo di Hadamard non fornisce alcun risultato utile circa la congettura di Riemann. Anzi, sembra suggerirne una negazione giacché ci si aspetta una parte reale degli zeri non banali variabile nell'intervallo aperto (0,1) e non identicamente pari a 1/2. In ogni caso, rimangono alcuni lati oscuri riguardo la convergenza del prodotto infinito in cui la funzione ξ è fattorizzata. Stiamo parlando dei singoli fattori in cui la variabile z non dipende dall'indice della produttoria. Per essere più specifici, il singolo fattore contiene la funzione -z moltiplicata per il reciproco del k-esimo zero non banale. Imponendo la convergenza assoluta è necessario lavorare sulle corrispodenti serie di funzioni, che per quanto precede non sono tali nel senso che si riducono al prodotto di -z per una serie numerica (e quindi, nono di funzioni) i cui termini sono i reciproci degli zeri non banali.

Osserviamo che le argomentazioni che spinsero Riemann a formulare la sua congettura, probabilmente derivano dal fatto che la parte reale di singolo zero non banale deve essere una costante. Dalla simmetria della distribuzione degli zeri rispetto alla linea critica, segue necessariamente che l'unico valore possibile per tale costante è 1/2.

Per provare quanto appena detto, e cioè Re(ρ)=costante, si potrebbe procedere per assurdo, tenendo conto del Teorema di Hardy, secondo cui sulla linea critica cadono infiniti zeri non banali. La negazione dell'ipotesi di Riemann implica che esistono almeno 4 zeri non banali non appartenenti alla linea critica la cui parte immaginaria è compresa tra le parti immaginarie di una assegnata coppia di zeri appartenenti alla linea critica. Si può generalizzare ipotizzando 4n zeri per un dato n intero naturale positivo, ma che comunque non può divergere, altrimenti per il Teorema di Bolzano-Weierstrass l'insieme H degli zeri non banali avrebbe almeno un punto di accumulazione. E ciò contraddice una nota proprietà dell'insieme degli zeri di una funzione olomorfa.

Tags: congettura di riemann, ipotesi di Riemann, sviluppo di hadamard, zeri non banali