[¯|¯] Sviluppo di Taylor della funzione xi di Riemann

Agosto 27th, 2019 | by Marcello Colozzo |

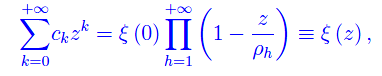
funzione intera,funzione xi di riemann,serie di taylor

è banale giacché per un noto teorema, ogni trascendente intera ammette uno sviluppo di Taylor con raggio di convergenza infinito. Viceversa, la somma di una qualunque serie di Taylor con raggio di convergenza infinito, è una trascendente intera. Nell'equazione appena scritta riconosciamo a primo membro lo sviluppo di Taylor di punto iniziale z=0 e di raggio di convergenza

Per quanto precede:

Inoltre dalla teoria delle variabili complesse, sappiamo che i coefficienti della serie di Taylor si esprimono come (γ è una circonferenza di centro l'origine e raggio arbitario):

oltre che attraverso la nota formula

Scriviamo

dove

dove l'ultimo termine è manifestamente il prodotto parziale di ordine n. Tali coefficienti dipendono dalle n variabili

per cui scriviamo

ed eseguendo il predetto limite

Deve essere

A questo punto, possiamo sfruttare la nota simmetria degli zeri della ξ(z) rispetto all'asse reale e alla retta critica

Da ciò segue che comunque prendiamo

si ha

D'altra parte lo sviluppo in prodotto infinito può scriversi

Cioè

avendo definito

Abbiamo così implementato un ordinamento degli zeri, e il corrispondente prodotto parziale di ordine 4n, che è manifestamente un polinomio di grado 4n, si scrive:

Ciò che a noi interessa è la parte reale di ρ_h^j, per cui l'unico parametro libero è Δ_h che misura la distanza assoluta dalla retta critica, onde la condizione di raggio di convergenza infinito della sviluppo in serie di Taylor, per la funzione ξ(z) si scrive