[¯|¯] Superfici di livello di un campo scalare

Luglio 30th, 2019 | by Marcello Colozzo |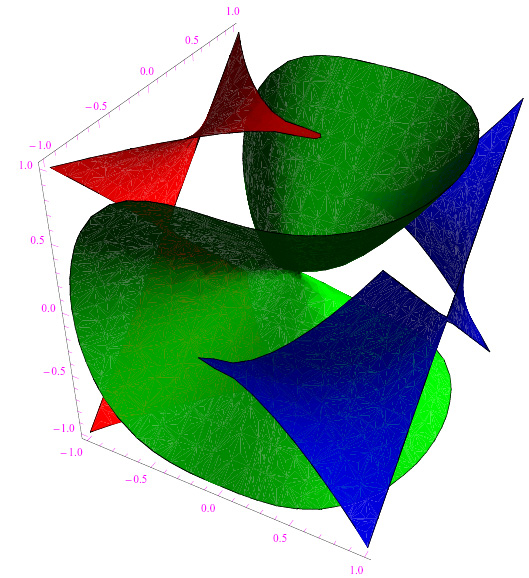

campo scalare,superfici di livello — **Fig. 1**

In Analisi vettoriale un campo scalare è una funzione reale delle variabili reali (x,y,z) quali coordinate cartesiane (Ovviamente si possono utilizzare altri sistemi di coordinate) in un riferimento cartesiano dello spazio ordinario. Quindi:

dove l'insieme di definizione D può essere un dominio di R³ o un qualunque insieme aperto (campo). Nelle applicazioni, la funzione U si assume sufficientemente regolare in D, cioè è ivi continua fino alle derivate parziali del second'ordine.

Ciò premesso, le superfici di livello di un campo scalare U(x,y,z) sono i luoghi geometrici:

essendo C una costante assegnata ed appartenente al codominio della funzione U(x,y,z). Nei casi più semplici, è facile esplicitare la tipologia di tali superfici. Ad esempio, le superfici del campo scalare

sono

cioè coni a due falde passanti per l'origine. Nel caso del campo

si può utilizzare l'istruzione ContourPlot3D di Mathematica, ottenendo le superfici plottate in fig. 1.

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Indice delle lezioni

No TweetBacks yet. (Be the first to Tweet this post)