[¯|¯] Generalizzazione del modello preda-predatore di Lotka-Volterra

Giugno 17th, 2019 | by Marcello Colozzo |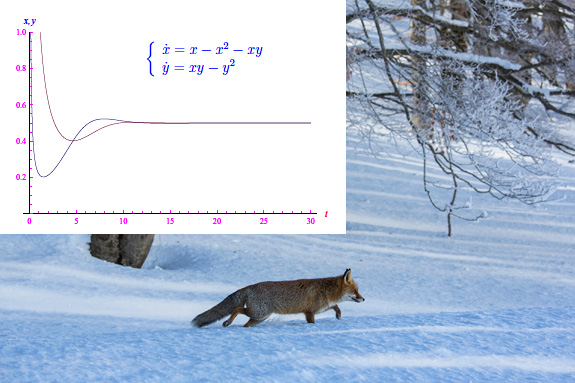

modello preda-predatore di Lotka-Volterra,mathematica,brown noise

In quest'articolo proponiamo una generalizzazione del modello preda-predatore di Lotka-Volterra. Precisamente, denotando con x(t) e y(t) le popolazioni (opportunatamente normalizzate) in funzione del tempo di un ecosistema a due componenti ove x rappresenta la preda e y il predatore, si ha:

dove abbiamo denotato le derivate rispetto al tempo utilizzando la notazione puntata. Per semplicità assumiamo pari a 1 i singoli coefficienti di proporzionalità, per cui

che compongono un sistema di due equazioni differenziali del primo ordine. Osserviamo che in entrambe, il termine quadratico -x² (o -y²) rappresenta l'interazione con l'ambiente, nel senso che quest'ultimo dispone di una quantità limitata di risorse. Diversamente e in assenza di predatori, il sistema precedente si riduce all'equazione differenziale

ovvero a una crescita esponenziale e^t. Di contro, la quantità limitata di risorse determina una diminuzione della velocità di crescita in entrambe le popolazioni. Al sistema precedente, vanno aggiunte le condizioni iniziali

onde viene a definirsi un problema di Cauchy compatibile e determinato. Assumendo x₀=y₀=7 e risolvendo tale problema con Mathematica, otteniamo il grafico:

Da tale diagramma vediamo che dopo un transitorio iniziale, il sistema tende a una configurazione di equilibrio in cui il numero di prede è pari al numero di predatori.

Si noti che la configurazione di equilibrio viene raggiunta anche se il numero iniziale di predatori è maggiore del numero di prede, come illustrato nel grafico della seguente figura ove è x₀=7, y₀=27.