[¯|¯] Software da combattimento aereo (esercizio di dinamica del punto materiale)

Febbraio 13th, 2019 | by Marcello Colozzo |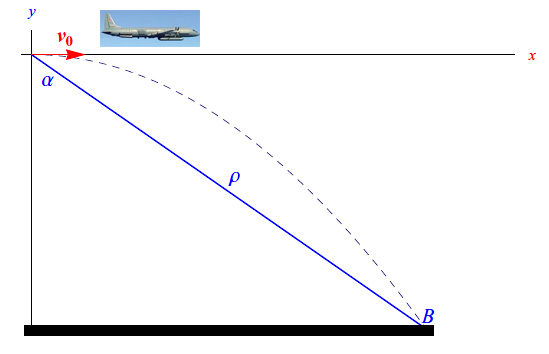

combattimento aereo,software,dinamica del punto materiale — **Fig. 1**

Esercizio
Trascurando la resistenza dell'aria e la curvatura terrestre, si consideri il moto di un aereo a quota h=225m e con velocità "orizzontale" costante v₀=155km/h . Il software di visualizzazione di un bersaglio B fermo sulla superficie terrestre, restituisce le coordinate polari (ρ,φ) di B, rispetto a un riferimento polare di polo la posizione istantanea dell'aereo, e di asse polare l'asse parallelo e concorde al vettore v₀, passante per la posizione istantanea dell'aereo, come illustrato in fig. 1, dove abbiamo istituito un sistema di riferimento K(Oxy) solidale alla Terra, e che può essere considerato con buona approssimazione inerziale.
Nello specifico, il software restituisce l'angolo α (fig. 1) che chiamiamo "angolo di visuale del bersaglio". Scrivere l'algoritmo utilizzato dal predetto software, il cui output è il valore α₀ di α, affinché un ordigno sganciato all'istante t=0, colpisca il bersaglio. Infine, graficare l'andamento di α₀ in funzione della quota h.

Soluzione

È ovvio che la traiettoria dell'ordigno è univocamente determinata dal modulo della velocità orizzontale. Infatti, le equazioni orarie dei singoli moti componenti lungo gli assi coordinati (che compongono una rappresentazione parametrica della traiettoria), sono:

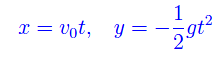
Al solito, eliminiamo il parametro t in modo da ottenere una rappresentazione cartesiana della traiettoria, ovvero della parabola:

Dalla fig. 1 si ricava immediatamente

L'ascissa del bersaglio è soluzione dell'equazione

da cui scartando la soluzione < 0 in quanto priva di significato fisico, otteniamo

onde

che è il valore restiuito dal software. Per rispondere all'ultimo quesito, osserviamo che la funzione a0(h) è infinitesima all'infinito:

Precisamente, eseguendo uno studio di funzione, otteniamo l'andamento di figura:

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.