[¯|¯] La dinamica nonlineare del cancro
Febbraio 7th, 2019 | by Marcello Colozzo |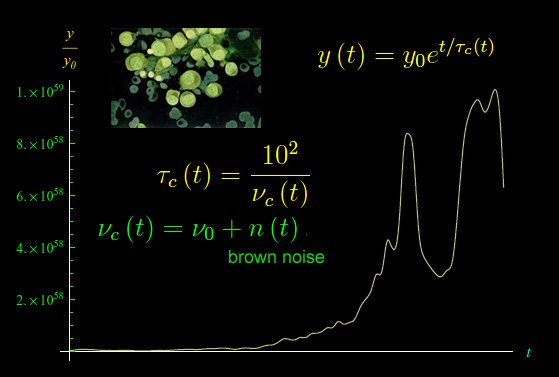
Sia Ω un organismo biologico. Nel paradigma del riduzionismo, Ω è un insieme di tessuti organici. Formalmente possiamo scrivere:

essendo ωk il k-esimo tessuto componente. A sua volta, ωk è costituito da Nk cellule, di cui una frazione macroscopica si moltiplica (incrementando Nk), mentre un'altra frazione muore. In altri termini, l'intero naturale Nk è una funzione del tempo. Denotando con y tale variabile, si ha:
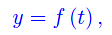
cioè abbiamo una funzione reale della variabile reale "tempo", denotata con t. Si noti che y appartiene al campo reale R, mentre Nk=[y], ove [·] simboleggia la parte intera di un numero reale. Riguardo all'espressione analitica della funzione f(t), ci aspettiamo differenti leggi, e in linea di principio tale funzione può essere monotanamente crescente (crescita di ωk) o monotonamente decrescente (decrescita di ωk). In generale, f(t) può essere monotona solo localmente. Le differenti leggi che esprimono la dinamica di ωk, possono essere inglobate in un'unica legge di tipo esponenziale, in cui l'argomento dell'esponenziale è modulato da un termine 1/τc(t). Precisamente:
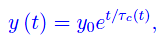
dove y0 è la popolazione di cellule ad un opportuno istante iniziale t0=0. Si noti che se τc(t) si riduce a una costante τ0, l'equazione precedente esprime una crescita esponenziale pura. La funzione τc(t) individua l'intervallo di tempo oltre il quale si ha una variazione apprezzabile della grandezza y(t). Per convincersene, è sufficiente considerare i casi estremi:
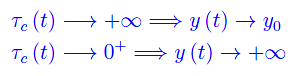
Nel primo caso, la popolazione di cellule è invariante per evoluzione temporale. In linea di principio ciò potrebbe rappresentare la morte di ωk, giacché non c'è né creazione né distruzione di cellule (tutti i processi organici sono congelati). Nel secondo caso, invece, abbiamo una crescita esponenzialmente infinita, che un comportamento patologico non rappresentabile da una funzione in senso ordinario. È però evidente che τc(t) fissa la scala dei tempi di ωk, giacché nel primo caso deve trascorrere un tempo infinito per osservare una variazione di y(t). Di contro, nel secondo caso la scala dei tempi è istantanea.
Definizione
La grandezza τc(t) è il tempo caratteristico del processo y(t) che caratterizza la proliferazione cellulare di ωk.
La funzione y(t) è soluzione di una equazione differenziale del primo ordine non lineare
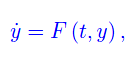
mentre la presenza di τc(t) nella predetta soluzione, suggerisce che tale grandezza è a sua volta soluzione di una qualche equazione differenziale non lineare. Tuttavia, possiamo congetturare che τc(t) sia in qualche modo correlata a un'altra grandezza con le dimensioni di una frequenza. Alcune particolarità di tipo biologico, suggeriscono che quest'ultima grandezza sia collegata alla frequenza cardiaca di Ω. Ad esempio, è stato congetturato che il ritmo cardiaco fissa la scala dei tempi di Ω. Un esempio clamoroso è dato dalla tartaruga, la cui longevità sarebbe una conseguenza della bassa frequenza cardiaca (6 battiti al minuto). Da un punto di vistga formale, possiamo scrivere:
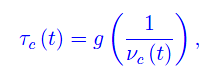
dove g è una funzione monotonamente crescente, mentre νc(t) è la frequenza cardiaca di Ω, che è data, a meno di un noise, da un termine mediato nel tempo:

dove
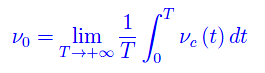
Considerando in particolare un brown noise, abbiamo per la frequenza un andamento del tipo di quello riportato in fig. 2.

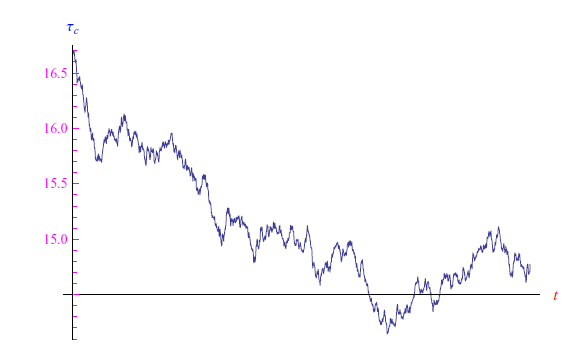
Assumiamo come tempo caratteristico dell'evoluzione della popolazione di cellule del tessuto ω{k} appartenente a Ω=tartaruga, la variabile aleatoria:
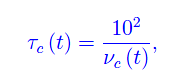
graficata in fig. 3.
A questo punto possiamo finalmente graficare la grandezza y(t) normalizzata su y0, come mostrato dalla fig. 1.
Tags: cancro, dinamica nonlineare, esponenziale, tempo caratteristico
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











