» Esercizi svolti di Matematica e Fisica

[¯|¯] Un baule sale, l'altro scende (lungo un piano inclinato)

Dicembre 11th, 2018 | by Marcello Colozzo |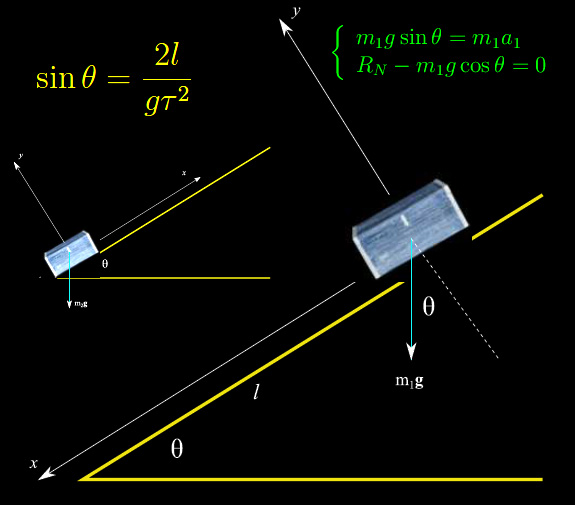

---

Esercizio

Dalla cima di un piano inclinato di lunghezza l privo di attrito, si lascia andare un baule che raggiunge il fondo dopo un tempo τ. Dal fondo del piano nel medesimo istante in cui viene lasciato il primo baule, viene lanciato un secondo baule su per la superficie inclinata con velocità tale che il predetto baule, riscendendo giunge di nuovo in fondo simultaneamente al primo. Determinare:
1)l'accelerazione di ciascun baule nella direzione del moto;
2)la velocità iniziale del secondo baule;
3)la distanza percorsa in salita dal secondo baule.

---

Soluzione
Quesito 1

Per lo studio del moto del primo baule, fissiamo un sistema di assi cartesiani come illustrato in fig. 1. Denotando con m₁ la massa del baule, il secondo principio della dinamica restituisce la seguente equazione vettoriale

essendo R_N la reazione vincolare normale, mentre a₁ è il vettore accelerazione lungo la direzione del moto.










Proiettando la predetta equazione vettoriale sugli assi cartesiani:

da cui possiamo ricavare l'accelerazione scalare:

L'equazione oraria del moto componente lungo l'asse x è

Deve essere

che ci consente di ricavare θ

Passiamo al secondo baule, schematizzato in fig. 1. Indicando con m₂ la massa del secondo baule, e applicando nuovamente il secondo principio della dinamica:

Come c'era d'aspettarsi, il modulo del vettore accelerazione (nella direzione del moto) è lo stesso di quello del primo baule, giacché il predetto modulo dipende solo dall'angolo di inclinazione. Quindi

---

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

---

Quesito 2
Per il secondo baule, l'equazione oraria del moto componente lungo l'asse x si scrive:

dove v₀ è la velocità iniziale. Si noti che abbiamo posto t=0 nell'istante in cui il secondo baule viene lanciato sul piano inclinato che per quanto precede, è l'istante in cui il primo baule viene lasciato. Inoltre, il secondo baule raggiungerà un'ascissa x(t₁)=d in un istante tt₁ che è manifestamente un istante di arresto con inversione del moto. Cioè

da cui

Il tempo richiesto per tornare in x=0 è ancora t₁. Ne consegue che il tempo di salita-discesa è 2t₁. Per ipotesi entrambi i bauli arriveranno in fondo al piano inclinato nel medesimo istante, onde:

Cioè

Quesito 3
L'equazione oraria per il secondo baule può essere riscritta

La distanza percorsa lungo il piano inclinato è



Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: accelerazione, baule, piano inclinato, velocità iniziale

Articoli correlati