» Esercizi svolti di Matematica e Fisica

[¯|¯] Esperimenti computazionali con il white noise

Giugno 21st, 2018 | by Marcello Colozzo |

In un post precedente abbiamo visto che la funzione di autocorrelazione di una variabile aleaotoria gaussiana, è una funzione SINC.
In sostanza, la funzione di autocorrelazione ci dice come sono correlati a tempi diversi i valori di una assegnata grandezza (aleatoria o deterministica). È chiaro che se la predetta funzione è identicamente nulla o più precisamente, una funzione delta di Dirac, allora i valori della variabile aleatoria sono scorrelati al 100%. È proprio quello che succede in un white noise. Per verificarlo, utilizziamo Mathematica. Definiamo una funzione random[] che genera numeri reali pseudocasuali:

Generiamo una lista di lunghezza n, di tali numeri:

Utilizziamo l'istruzione ListLinePlot[] per plottare la lista:

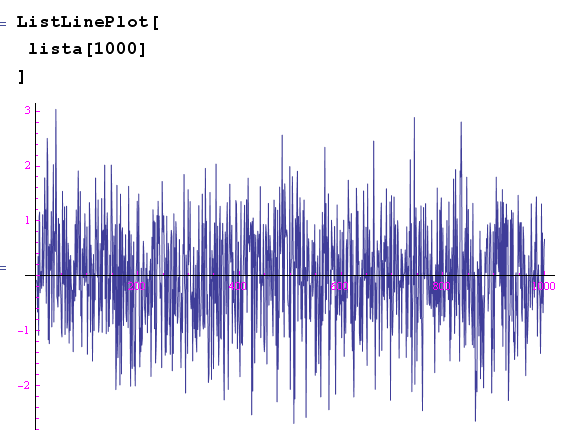
Alternativamente, interpoliamo:


L'integrazione della funzione α(t) genera un Brown Noise. Nel grafico di fig. 1 sono confrontati i grafici del white noise, del brown noise e di una funzione di tipo sinusoidale.

Tags: brown noise, distribuzione gaussiana, white noise

Articoli correlati