[¯|¯] Applicazione inversa
Giugno 11th, 2018 | by Marcello Colozzo |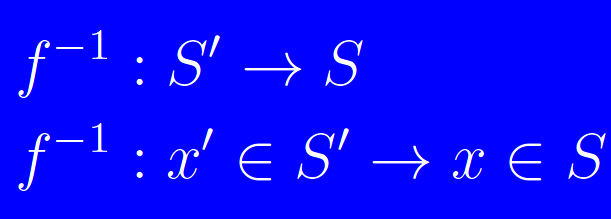
Comunque prendiamo un'applicazione bi-iettiva f:S->S', è univocamente determinata l'applicazione che associa all'elemento x' di S', l'elemento x di S tale che f(x)=x'. Infatti, l'iniettività implica l'unicità dell'elemento x:
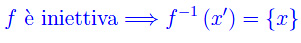
Definizione
Chiamiamo applicazione inversa la predetta applicazione, denotandola con f-1 e scrivendo:
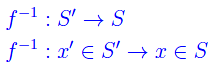
Proposizione
Comunque prendiamo una biezione f:S'->S, si ha
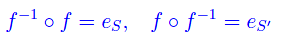
Dimostrazione
onde
In maniera analoga si dimostra l'altra relazione.
Proposizione
Ipotesi: Per un'assegnata applicazione f:S->S', esiste un'applicazione g:S'->S tale che
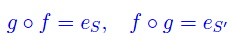
Tesi:
- f è una biezione
- g=f-1
Dimostrazione
Iniziamo con il dimostrare che f è bi-iettiva i.e. è suriettiva e iniettiva. Sia
Segue
In virtù dell'arbitrarietà di x' quale elemento di S', si ha
onde la suriettività di f.
Per dimostrare l'iniettività prendiamo
per cui
Cioè f è iniettiva. Per dimostrare il punto 2, consideriamo
Per la proprietà associativa
da cui l'asserto.
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Articoli correlati

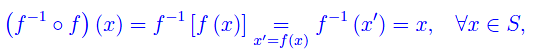
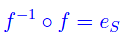
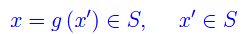
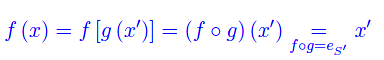
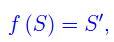
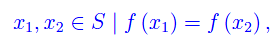
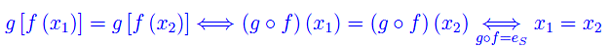
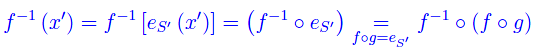
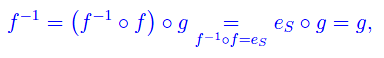


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











