[¯|¯] Definizione di insieme. Il paradosso di Russell
Giugno 5th, 2018 | by Marcello Colozzo |
Un insieme è un "Molti" che si lascia
pensare come un "Uno"
G. Cantor, 1883
Prima di passare alla definizione di insieme e al paradosso di Russel, citiamo alcuni brani del libro La mente e l'infinito del matematico e scrittore Rudy Rucker
Proviamo a pensare al Tutto, all'universo passato e presente nella sua interezza, a tutti gli universi possibili, a tutti i possibili pensieri, a tutti gli insiemi di enti matematici.
Si può pensare a tutto ciò? Il classico problema Uno/Molti nasce dalla seguente domanda: il Tutto può essere considerato come un singolo oggetto, come un'unità? Il mondo è un Uno o un Molti?
[...]C'è tuttavia un desiderio inesauribile di ridurre la molteplicità dei fenomeni del mondo a un unico tipo fondamentale, di credere che in ultima analisi tutte le cose siano fatte della stessa sostanza. Materia, sensazione, pensiero e forma sono stati tutti candidati per la qualifica di "Urstoff", di materia primordiale. La credenza che vi sia in ultima analisi un solo tipo di oggetti nel mondo è detta "monismo dei generi".
[...]
Invece di formare unità comprendenti molteplici oggetti a partire dal basso, si può partire dall'alto usando l'asserzione "Tutto è Uno". Il monismo della sostanza asserisce che ogni cosa è una parte o una manifestazione di un'unità superiore che è usualmente chiamata l'Assoluto.
La nozione di elemento è assunta come primitiva, ossia non riconducibile a concetti più semplici. Il termine oggetto è spesso utilizzato come sinonimo di elemento.
Allo stesso modo, quella di totalità o classe di oggetti, è una nozione primitiva.
Esempio
Gli alunni presenti in un'aula costituiscono una "classe" i cui elementi sono i singoli alunni.
Definizione
Dicesi insieme una classe tale che esista una legge che sia in grado di stabilire l'appartenenza o la non appartenenza di un elemento alla classe medesima.
Esempio
In un piano α sia data una circonferenza γ di centro Ω e raggio R. I punti di γ costituiscono un insieme, giacché è univocamente definita la legge di appartenenza:
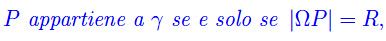
essendo |ΩP| la misura assoluta del segmento ΩP.
Per evitare il paradosso di Russel, formuliamo la seguente definizione:
Definizione
Un insieme normale è un insieme che non contenga sé stesso come elemento. Un insieme anormale è un insieme che contenga sé stesso come elemento.
A questo punto, manteniamo distinte le nozioni di insieme e di classe di oggetti. Dimostriamo la seguente proposizione:
Proposizione
Ipotesi: N è la classe degli insiemi normali
Tesi: N non è un insieme.
Dimostrazione
Procediamo per assurdo. La negazione della tesi è:
N è un insieme Segue che N appartiene a sé stesso come elemento, giacché per definizione N è la classe degli insiemi normali. Quindi N contiene sé stesso come elemento, per cui N è un insieme anormale, contraddicendo l'assunto iniziale.
Assumiamo ora che N sia un insieme anormale. Ciò implica necessariamente l'appartenenza di N a sé stesso come elemento. Ma N è per definizione la classe degli insiemi normali, per cui se N appartiene (come elemento) a N, ne consegue che N è normale, contraddicendo l'assunto precedente, onde l'asserto.
Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: definizione di insieme, paradosso di russel, Rudi Rucker
Articoli correlati



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico









