[¯|¯] La componente di un vettore secondo una retta orientata
Giugno 2nd, 2018 | by Marcello Colozzo |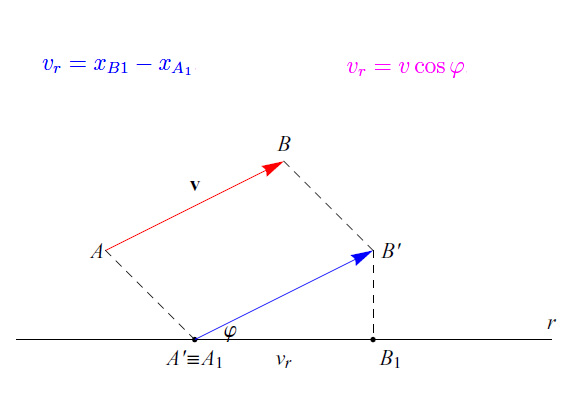
Consideriamo un vettore libero v e una retta orientata r. Se il vettore v è rappresentato da un segmento orientato AB appartenente a una retta non complanare ad r, assumiamo come segmento rappresentativo di v un segmento orientato A'B' complanare ad r e disposto come in fig. 1. Denotiamo con A1=A' e B1 i piedi delle perpendicolari condotte ad r per A e B o ciò che è lo stesso, per A' e B'.
Definizione
La componente di v secondo la retta r è il numero reale
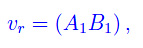
dove (A1B1) denota la misura relativa del segmento orientato A1B1:

e
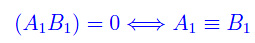
Introducendo in r un riferimento cartesiano R(Ox) ovvero un sistema di ascisse, si ha
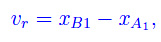
dove xA1 e xB1 denotano le ascisse di A1 e B1 rispettivamente. Denotando con φ l'angolo che la retta orientata r forma con il segmento orientato A'B', otteniamo l'evidente espressione
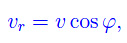
da cui discende la seguente condizione necessaria e sufficiente affinché si annulli vr:
Se v è un vettore non nullo

Sostienici



 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











