[¯|¯] Applicando la regola di De L'Hospital dopo aver eseguito un cambio di variabile

Maggio 31st, 2018 | by Marcello Colozzo |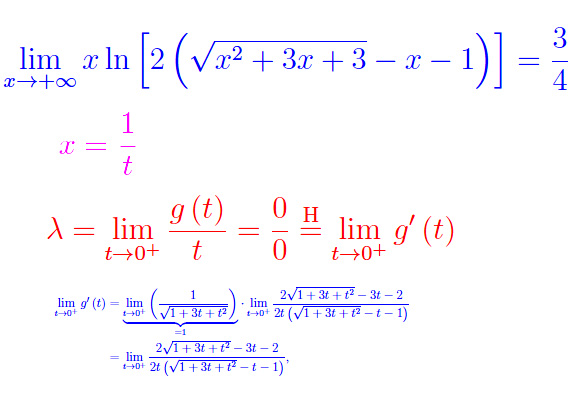

limite, funzione,regola di de l'hospital,cmabio di variabile

Il procedimento appena visto cioè lo sviluppo di Mac Laurin per rimuovere la forma indeterminata, in realtà equivale ad applicare la regola di De L'Hospital dopo aver eseguito il cambio di variabile x=1/t. Per mostrare ciò riferiamoci al seguente caso:

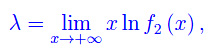
limite, funzione,regola di de l'hospital,cmabio di variabile

con la solita ipotesi
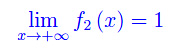
limite, funzione,regola di de l'hospital,cmabio di variabile

Se poniamo

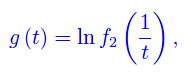
limite, funzione,regola di de l'hospital,cmabio di variabile

si ha

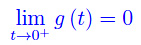
limite, funzione,regola di de l'hospital,cmabio di variabile










Il caso che stavamo considerando è

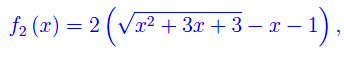
limite, funzione,regola di de l'hospital,cmabio di variabile

onde

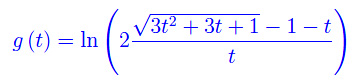
limite, funzione,regola di de l'hospital,cmabio di variabile

Calcoliamo la derivata prima:

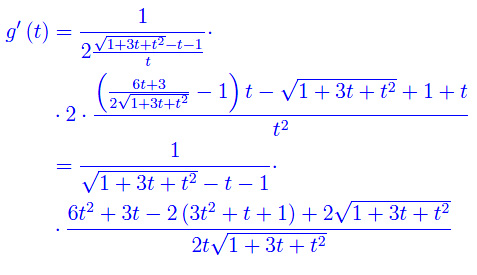
limite, funzione,regola di de l'hospital,cmabio di variabile

Semplificando
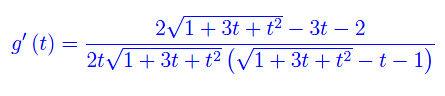
limite, funzione,regola di de l'hospital,cmabio di variabile

Eseguiamo l'operazione di passaggio al limite:

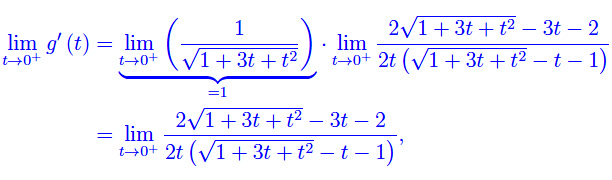
limite, funzione,regola di de l'hospital,cmabio di variabile

che si presenta nella forma indeterminata 0/0. Anziché applicare De L'Hospital, eseguiamo le seguenti manipolazioni:
limite, funzione,regola di de l'hospital,cmabio di variabile


Sostienici







No TweetBacks yet. (Be the first to Tweet this post)

Tags: , , ,

Articoli correlati

Commenta l'esercizio