» Esercizi svolti di Matematica e Fisica

[¯|¯] Cosa è una funzione?

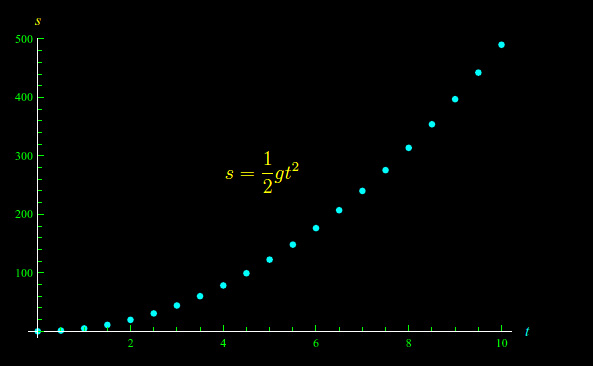
Supponiamo di far cadere una moneta da un torre, e di rilevare per certi istanti di tempo quanto spazio ha percorso dalla nostra mano, per esempio dopo un secondo avrà percorso 4.9 metri, dopo due secondi 19.62 metri , etc etc.

Questi non sono altro che dati, per ottenere altri dati devo fare altre rilevamenti, ovvero immetto secondi e metri in una tabella:

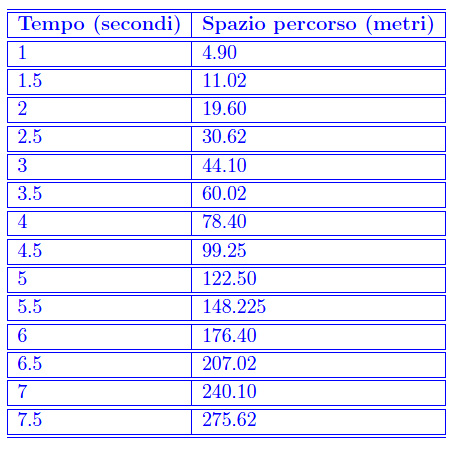
Tali dati possono essere graficati. Precisamente, se in ascisse riportiamo il tempo espresso in secondi, e in ordinate lo spazio percorso in metri, otteniamo il diagramma riportato in fig. 1.

Il predetto procedimento non è molto pratico. Ora immaginate che arrivi qualcuno e ci comunichi che ha scoperto la legge che collega questi due dati, cioè:

Ovvero che lo spazio percorso in un determinato tempo dipende dalla metà della accelerazione di gravità g per il quadrato del tempo impiegato. La prima cosa da fare è verificare che sia effettivamente così, si fa una verifica dati alla mano. Una volta effettuata questa verifica e ci si accerta che tale legge rispecchia il fenomeno appena descritto, ecco che ho una funzione. Quale è il vantaggio? Il vantaggio è che adesso posso descrivere il fenomeno senza rilevare dati, ma solo specificando i valori della variabile indipendente t. Non ho più bisogno di dire a questo tempo tot corrisponde uno spazio percorso tot, perché, conoscendo la legge che li collega è sufficiente immettere il tempo e, facendo i calcoli, ottengo lo spazio percorso. In poche parole, la funzione si può paragonare a una macchina che fa il lavoro nostro programmandola, noi la programmiamo mettendoci dei dati, e lei ci fornisce i relativi stati dell'evento per i dati che abbiamo fornito.

Facciamo un ulteriore esempio: Un ciclista percorre una pista circolare, con raggio di R=2m , ed un osservatore al centro rileva quanto spazio percorre il ciclista in relazione all'angolo formato con il diametro passante per il punto di partenza, misurato in radianti:

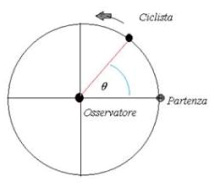
Sapendo che per 30° (π/6 radianti) avrà percorso π/3 m , per 45° (π/4 radianti) ha percorso π/2 m , e che per un angolo di 90° (π/2 radianti) avrà percorso esattamente π m.

Sono solo dati, ma se qualcuno ci informasse che: tra lo spazio s percorso dal ciclista e l'angolo formato θ vi è la relazione: s=πRθ, non ci servirebbe più la tabella, poiché, conoscendo il raggio della pista e l'angolo formato, basta moltiplicare questi per il numero π ed il gioco è fatto: abbiamo lo spazio percorso dal ciclista. Questo tipo di funzione in cui possiamo scrivere una legge che collega i dati in entrata e quelli in uscita, si dice analitica; premettiamo da subito che non tutte le funzioni sono analitiche, alcune anche in modo sorprendente. Ma procediamo per passi, e per ora fermiamoci qui.

Scarica la lezione in formato pdf

Tags: analisi matematica, Cinematica, funzione