» Esercizi svolti di Matematica e Fisica

[¯|¯] Integrazione per quadrature (equazioni differenziali del primo ordine)

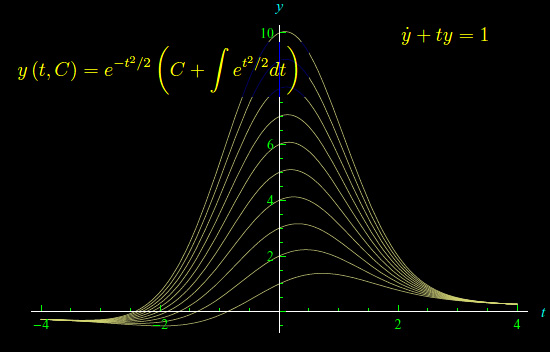
Il prossimo capitolo del volume II del ciclo Degeometrizzando eternamente potrebbe essere intitolato "L'algoritmo ignoto", ovvero uno "schema di calcolo" che metaforicamente, accetta dati reali e sputa nella realtà fisica dati "transreali" (cioè visionari).

Bisognerebbe poi implementare una "tecno-poesia" dedicata alla maggioranza silenziosa dei sistemi dinamici non integrabili "per quadrature", e come tali non elementarmente esprimibili. I "realisti" conoscono esclusivamente ciò che è tangibile, ossia (nel caso in esame) circuiti serie del tipo RC/RL (e altro), quindi caratterizzati da sistemi dinamici integrabili per quadrature. Ma il substrato dell'Universo è di natura matematica, per cui anche i sistemi non elementarmente esprimibili hanno diritto di esistenza. Magari non modellizzano alcun ente fisico, ma ciò non ha importanza, in quanto allocati in Platonia, l'unica realtà oggettiva.

Nella figura: un sottoinsieme della famiglia integrale di un banale sistema dinamico non integrabile per quadrature: y'+t*y=1. In altre parole, la procedura "per quadrature" fallisce anche nei casi più semplici.

scarica l'esempio in pdf

Tags: equazioni differenziali del primo ordine, integrazione per quadrature