» Esercizi svolti di Matematica e Fisica

[¯|¯] Una condizione necessaria e sufficiente per l'esistenza degli zeri non banali della zeta di Riemann

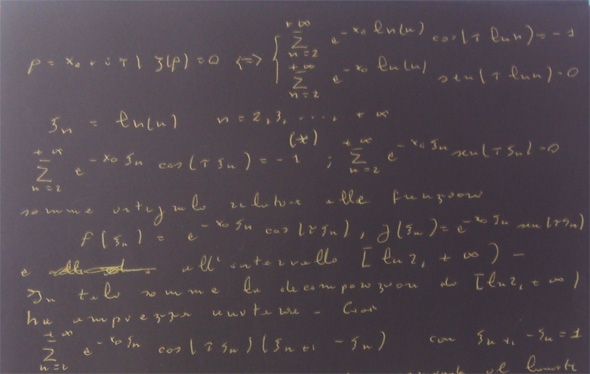
Penso di aver trovato una condizione necessaria e sufficiente per l'esistenza degli zeri non banali della funzione zeta di Riemann, come vediamo dalla fig. 1. Le condizioni si ottengono separando la parte reale e la parte immaginaria della zeta, e parametrizzando le variabili

Con un banale cambio di variabile, ci accorgiamo che le serie che esprimono la condizione sono, in realtà, somme integrali relative a due assegnate funzioni e all'intervallo illimitato [ln2,+oo). Sfortunatamente ciò non ci dice nulla al riguardo degli zeri, nel senso che gli integrali corrispondenti sono convergenti e si calcolano facilmente, ma nel caso in esame si hanno due somme integrali ottenute mediante una decomposizione dell'intervallo di integrazione in intervalli parziali di ampiezza unitaria. In alternativa, si potrebbe forzare il calcolo numerico delle somme, cercando di ricavare coppie di valori (x₀,τ), verificando se effettivamente riesce x₀=1/2 come esige la congettura di Riemann.

Tags: congettura di riemann, funzione zeta, zeri non banali