[¯|¯] La funzione zeta di Riemann e la propagazione di onde piane con velocità immaginaria
Gennaio 27th, 2018 | by Marcello Colozzo |
Abbiamo visto che parametrizzando in maniera opportuna le variabili indipendenti, la funzione zeta di Riemann, si esprime come sovrapposizione lineare di infinite onde stazionarie.
Di seguito alcune osservazioni.
- ψn(x+i*t) è olomorfa
- ψn(x,t) è dotata di derivate parziali di ordine comunque elevato e continue in C
in C={x+i*t | -oo
Per un noto teorema, segue (la condizione 2 è sovrabbondante, poiché è richiesta esistenza e continuità delle derivate parziali fino al secondo ordine) che

Da un punto di vista formale, la predetta equazione può scriversi nel piano xt, come un'equazione di D'Alembert:
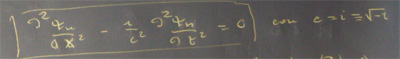
Come è noto, l'integrale generale di tale equazione è:
cioè la sovrapposizione lineare di due onde piane (una progressiva e l'altra regressiva) che si propagano a velocità immaginaria. D'altra parte, ψn(x,t) è un'onda stazionaria, ma in senso improprio poiché la stazionarietà implica comunque un'oscillazione della parte spaziale dell'onda.
Ma abbiamo visto che in un qualunque intervallo limitato [a,b] di R, la parte spaziale un(x,t) può essere sviluppata in integrale di Fourier, e quindi decomposta in oscillazioni sinusoidali nella variabile x. Ne consegue che la funzione zeta nasce dall'interferenza di infinite onde stazionarie. Se la somma infinita conserva il carattere stazionario dell'onda risultante, la zeta dovrebbe esprimersi come prodotto di due funzioni, di cui una dipendente solo da x, l'altra solo da t.
Tags: equazione di Laplace, funzione Zeta di Riemann, onde piane, onde stazionarie
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











