[¯|¯] Interpretazione quantistica della funzione zeta di Riemann
Gennaio 25th, 2018 | by Marcello Colozzo |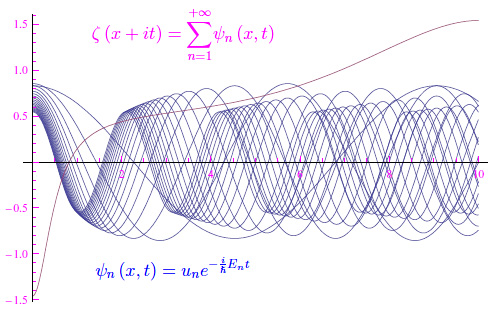
Proprietà
La funzione zeta di Riemann opportunatamente parametrizzata, è la somma della serie (più precisamente, per x<1 è un'estensione olomorfa) i cui termini sono le autofunzioni dell'energia di un sistema quantistico non relativistico, che compie un moto unidimensionale nella regione x>=0 sede di un campo di forze conservativo di energia potenziale V(x) formalmente definita dalla funzione impropria (barriera di potenziale): V(x)=+oo, se x<0.
CORREZIONE. La proprietà scritta in quel modo, è sbagliata perché il sistema di funzioni {u_n(x)} non è ortonormale, quindi non è una base ortonormale dello spazio di Hilbert L^2(R), e perciò non possono essere autofunzioni di un operatore hermitiano, quale è l'hamiltoniano di un sistema quantistico. Però sicuramente {u_n(x)} è linearmente indipendente, quindi può essere ortnormalizzato applicando il procedimento di Gram-Schmidt.
Per la dimostrazione di questa proprietà, scarica il pdf
Tags: autofunzioni dell'energia, barriera di potenziale, funzione Zeta di Riemann
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











