» Esercizi svolti di Matematica e Fisica

[¯|¯] Analisi armonica della zeta di Riemann

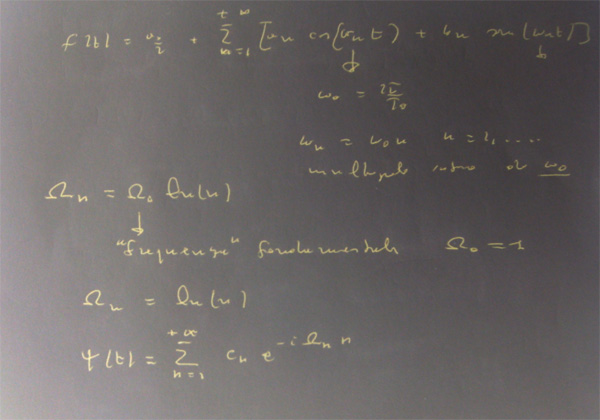
Ho cancellato il post precedente perché conteneva un errore, quindi le conclusioni erano sbagliate. Rimane comunque una somiglianza tra la serie di Dirichlet che definisce la restrizione della zeta di Riemann su una qualunque retta del piano complesso parallela all'asse immaginario (quindi, inclusa, la linea critica). Come vediamo nella fig. al top, la restrizione ψ(t) si decompone in infinite oscillazioni sinusoidali (armoniche), proprio come nella serie di Fourier, con la differenza sostanziale che la frequenza angolare dell'ennesima armonica non è un multiplo intero della frequenza dell'armonica fondamentale, ma varia con legge logaritmica. Lo spettro logaritmico delle frequenze distrugge la periodicità della somma della serie.

Ed è proprio ciò che ci si aspetta, visto che la ψ(t) tutto può essere tranne che una funzione periodica. Inifine, la presenza del logaritmo potrebbe essere casuale, oppure dovuta al fatto che la distribuzione dei numeri primi p(x) va asintoticamente come x/ln(x), tenendo presente che la distribuzione degli zeri non banali della zeta, determina la distribuzione dei numeri primi.