» Esercizi svolti di Matematica e Fisica

[¯|¯] Dimostrare per assurdo la congettura di Riemann?

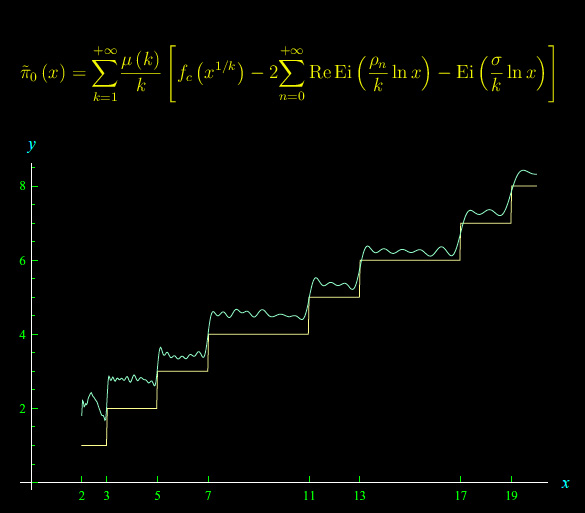
In un precedente ebook abbiamo utilizzato un approccio computazionale della Congettura di Riemann, scrivendo un programma in Mathematica e basandoci essenzialmente su un'analisi eseguita da due matematici svedesi nel 1970 sulla formula di Riemann - Von Mangoldt, che fornisce un'approssimazione della funzione di distribuzione dei numeri primi.

Ciò premesso, la congettura di Riemann potrebbe essere dimostrata per assurdo. Ricordiamo che nella dimostrazione per assurdo viene negata la tesi di una proposizione/teorema, e se ciò conduce a una negazione dell'ipotesi, allora il teorema è dimostrato. Alternativamente, la negazione della tesi potrebbe portare a una conclusione assurda, e ciò dimostra appunto la veridicità della tesi e, quindi, del teorema.

Nel caso della Congettura di Riemann, una negazione della tesi è realizzata assumendo l'esistenza di almeno uno zero non banale della zeta con parte reale diversa da 1/2. Se ciò conduce - attraverso una serie di passaggi logici - a una contraddizione per quel che riguarda una qualche proprietà della zeta, allora il teorema è dimostrato. Il problema è che la zeta è un oggetto tutt'alto che maneggevole, per cui occorre riferirci a qualcosa di più "semplice". E allora possiamo sfruttare la funzione reale della variabile reale x denotata con π₀(x) e che è appunto restituita dalla predetta formula di Riemann - Von Mangoldt. In parole povere, aggiungendo uno zero non banale con parte reale diversa da 1/2, la componente f_d(x) a secondo membro della formula, assume valori complessi, per cui la funzione π₀(x) non è più una funzione reale e come tale non può approssimare la distribuzione dei primi π(x).

Sostienici

Puoi contribuire all’uscita di nuovi articoli ed e-books gratuiti che il nostro staff potrà mettere a disposizione per te e migliaia di altri lettori.

Tags: Dimostrare per assurdo la congettura di Riemann