[¯|¯] Studio della traiettoria di una particella
Ottobre 12th, 2017 | by Marcello Colozzo |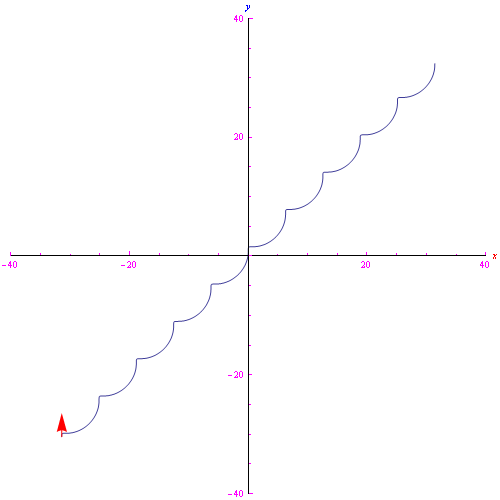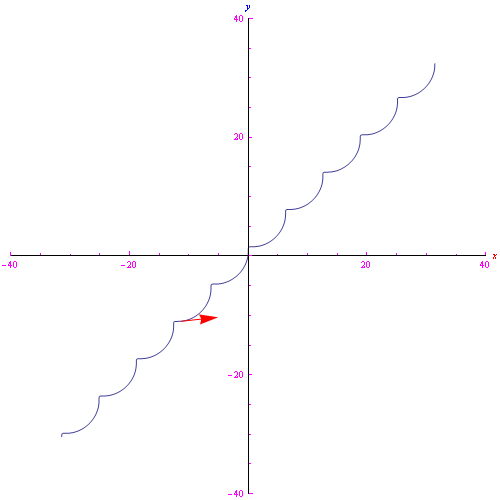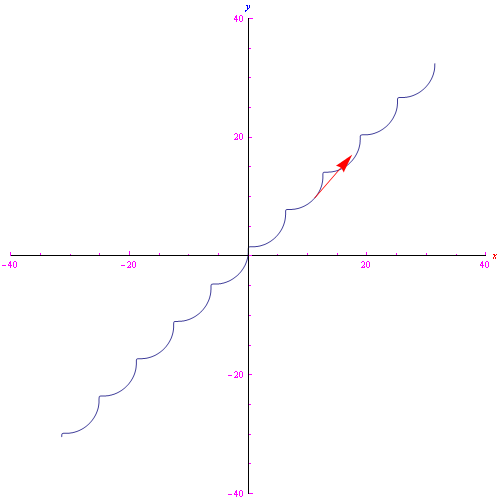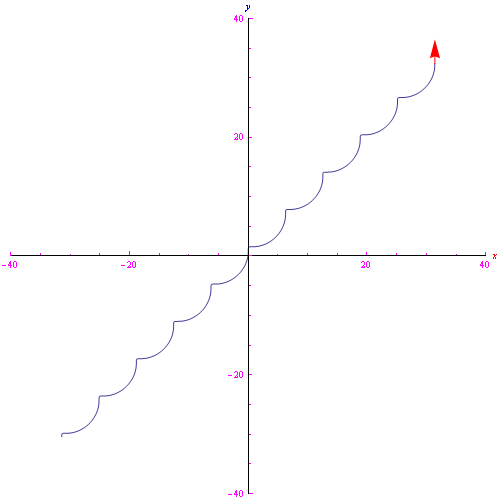
Studiare la traiettoria di una particella che compie un moto piano con equazione orarie (in unità adimensionali):
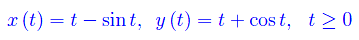
Soluzione
Le equazioni orarie determinano la seguente rappresentazione parametrica regolare
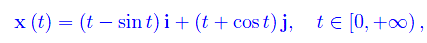
da cui calcoliamo la velocità vettoriale:

Da tale espressione segue

onde non esistono istanti di arresto. Determiniamo gli istanti in cui si annulla almeno una delle componenti cartesiane della velocità. La componente secondo l'asse x

In tali istanti il vettore velocità è parallelo all'asse y, mentre la posizione della particella è
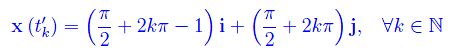
Cioè

Gli istanti in cui si annulla la componente di v secondo l'asse y:
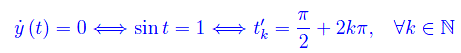
In tali istanti il vettore velocità è parallelo all'asse x, mentre la posizione della particella è
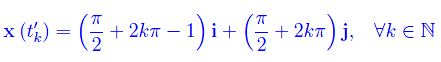
Cioè
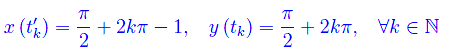
La posizione iniziale della particella è
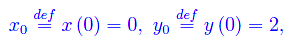
con il vettore velocità disposto lungo l'asse y. Per
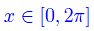
l'andamento della traiettoria è riportato in figura:
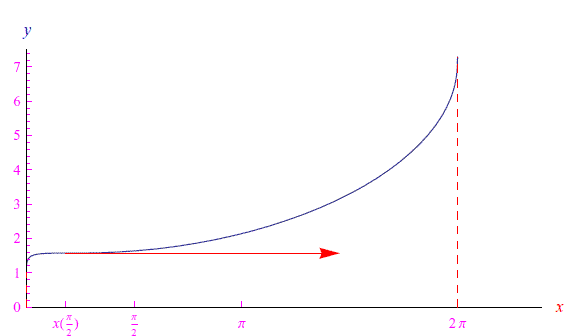
Mentre per
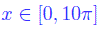
l'andamento è
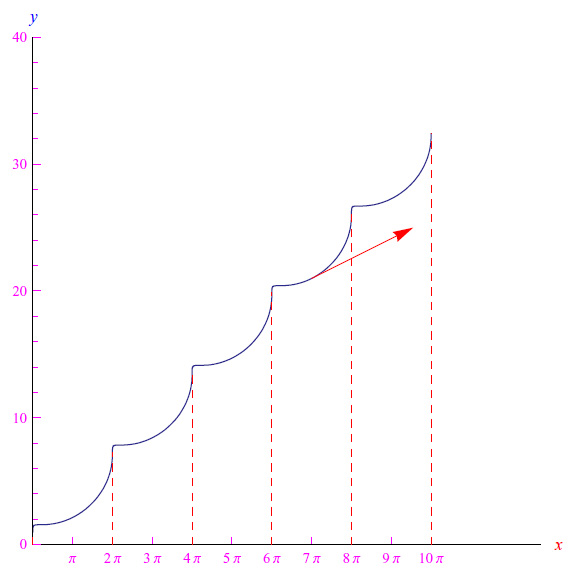
Sostienici
No TweetBacks yet. (Be the first to Tweet this post)
Tags: particella, traiettoria, vettore velocità
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











