[¯|¯] Le statistiche quantistiche applicate all'Universo primordiale
Agosto 8th, 2017 | by Marcello Colozzo |
Dall'equazione che esprime l'andamento della temperatura dell'universo primordiale, si ha che T(t->0)=+oo, poiché è a(0)=0.
Quindi in epoche primordiali ci aspettiamo una temperatura talmente alta da innescare la transizione al regime ultrarelativistico per ciò che riguarda il comportamento cinetico delle particelle che compongono il fluido cosmologico.
Dal punto di vista della teoria quantistica dei campi, si assiste al fenomeno della produzione di coppie particella-antiparticella. Per fissare le idee consideriamo una generica particella x di massa mx quando la temperatura dell'universo è tale che kBT=2mxc², il processo di annichilazione-creazione
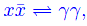
ha un equilibrio spostato verso destra. Per questi valori di temperatura il fluido è costituito da un elevato numero di coppie particella-antiparticella. Al crescere indefinito della temperatura, si creano coppie di particelle-antiparticelle sempre più massive.
Osserviamo che nella relazione precedente il limite t->0 costituisce una notazione formale, poiché per t=tP - tempo di Planck
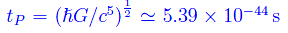
la Relatività Generale, "esce" dal suo dominio di validità, poichè gli effetti quanto-gravitazionali in tale intervallo di tempo non sono più trascurabili.Infatti la Relatività Generale è una teoria classica del campo gravitazionale, nel senso che non tiene conto degli effetti quantistici. Allo stato attuale delle conoscenze non esiste una teoria quantistica della gravità che sia logicamente chiusa, perciò quando scriviamo t->0, intendiamo t->tP. Oltre al tempo di Planck possiamo definire altre grandezze fisiche correlate ad esso. Osserviamo che l'orizzonte cosmologico a t=tP è pari a lP=ctP che è la lunghezza di Planck.
Possiamo così definire la massa di Planck come la massa dell'universo a tP, pari a
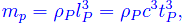
essendo ρP la densità dell'universo a tP. A questo punto ricordiamo che il tempo di Planck è l'intervallo di tempo durante il quale si hanno fluttuazioni dell'energia dell'ordine di mpc², che è l'energia di riposo dell'universo al tempo di Planck. Come è noto, tali fluttuazioni sono una conseguenza della relazione di indeterminazione di Heisenberg del tipo tempo-energia:
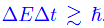
Quindi possiamo porre:
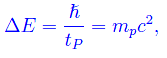
Sostienici
Tags: lunghezza di planck, massa di planck, universo primordiale
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











