[¯|¯] Esercizio sul prodotto scalare quale tensore covariante di rango 2
Giugno 3rd, 2017 | by Marcello Colozzo |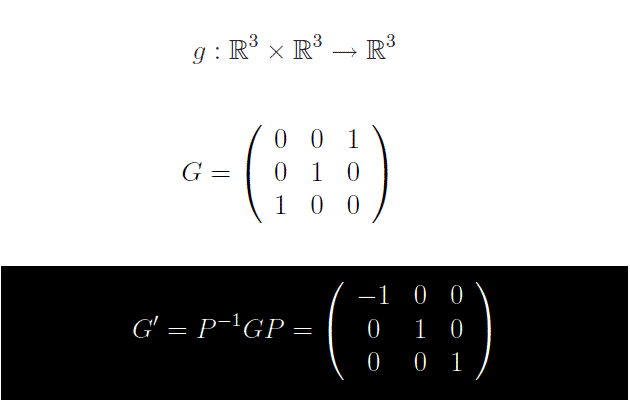
Esercizio
Studiare la forma bilineare illustrata in fig. 1.
Soluzione
Risulta
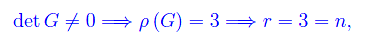
per cui la forma bilineare assegnata è un prodotto scalare. Per determinarne l'indice di positività conviene diagonalizzare la matrice G. Applichiamo quindi il procedimento standard di diagonalizzazione, determinando autovalori e autovettori. Gli autovalori sono le radici del polinomio caratteristico
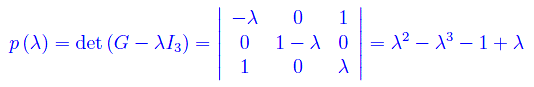
Quindi
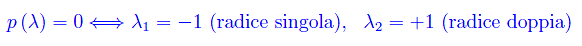
Le componenti degli autovettori corrispondenti all'autovalore -1 sono le soluzioni non banali del sistema omogeneo
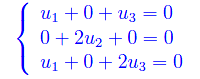
Una delle soluzioni è
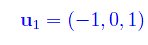
All'autovalore +1 di molteplicità algebrica 2 corrisponde il sistema di autovettori
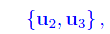
e a meno di un fattore di proporzionalità
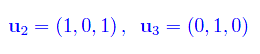
Abbiamo dunque la base {ui} di R³. La matrice G è diagonalizzata dalla matrice P di passaggio dalla base canonica alla nuova base.
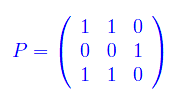
Precisamente
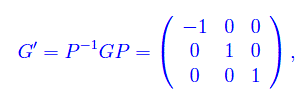
da cui vediamo immediatamente che l'indice di positività del prodotto scalare è p=2. Dal momento che p
No TweetBacks yet. (Be the first to Tweet this post)
Tags: forma bilineare, prodotto scalare, teorema di Sylvester
Articoli correlati


 Congettura di Riemann
Congettura di Riemann Trasformata discreta di Fourier
Trasformata discreta di Fourier
 Trasformata di Fourier nel senso delle distribuzioni
Trasformata di Fourier nel senso delle distribuzioni Trasformata di Fourier
Trasformata di Fourier  Infinitesimi ed infiniti
Infinitesimi ed infiniti Limiti notevoli
Limiti notevoli Punti di discontinuità
Punti di discontinuità Misura di Peano Jordan
Misura di Peano Jordan Eserciziario sugli integrali
Eserciziario sugli integrali Differenziabilità
Differenziabilità  Differenziabilità (2)
Differenziabilità (2) Esercizi sui limiti
Esercizi sui limiti Appunti sulle derivate
Appunti sulle derivate Studio della funzione
Studio della funzione Esercizi sugli integrali indefiniti
Esercizi sugli integrali indefiniti Algebra lineare
Algebra lineare Analisi Matematica 2
Analisi Matematica 2 Analisi funzionale
Analisi funzionale Entanglement quantistico
Entanglement quantistico Spazio complesso
Spazio complesso Biliardo di Novikov
Biliardo di Novikov Intro alla Meccanica quantistica
Intro alla Meccanica quantistica Entanglement Quantistico
Entanglement Quantistico











